Kiedyś w XXI wieku, gdy będę już zbyt stary, by móc powiedzieć coś pożytecznego na ten temat, młodsi fizycy będą musieli zdecydować, czy rzeczywiście odkryliśmy teorię ostateczną.
Edward Witten
Pięć teorii wszystkiego
John Schwarz i Michael Green narobili swoją pracą z lat 80. wiele szumu w świecie fizyki. Pokazali jak niedoszły opis oddziaływania silnego, daje się wykorzystać do realizacji jednego z najambitniejszych celów w dziejach nauki, czyli zjednoczenia wszystkich czterech oddziaływań. Ich wariacja teorii strun wciąż straszyła ogromem niedomówień i komplikacji, ale dała całemu pokoleniu badaczy nadzieję na udział w nowym, znaczącym rozruchu skostniałej fizyki. Ekstrawagancka hipoteza błyskawicznie wskoczyła na salony, stając się głównym tematem rozważań dla setek teoretyków. Poszczególne zespoły chłonęły pionierskie publikacje, próbując następnie na własną rękę wykorzystywać oferowaną przez struny elastyczność i geometrię wyższych wymiarów do tłumaczenia poszczególnych zjawisk. Najbardziej pożądanym i komfortowym finałem tego zrywu byłoby niezależne dojście różnych uczonych do identycznych lub przynajmniej zbliżonych wniosków. Otrzymanie bliźniaczych równań, automatycznie świadczyłoby o obraniu prawidłowej ścieżki, prowadzącej wprost do teorii wszystkiego.
Niestety nastąpiła sytuacja dokładnie odwrotna. Na horyzoncie zarysowało się aż pięć różnych teorii strun. Znawcy tematu okrasili je niezbyt literackimi nazwami: teorii heterotycznej SO(32), heterotycznej E8 × E8, typu I, typu IIA i typu IIB. Wszystkie wyglądały solidnie od strony matematycznej, wszystkie zastępowały punktowe cząstki obiektami rozciągłymi w przestrzeni i wszystkie korzystały z dziewięciu wymiarów przestrzennych (i jednego czasowego). Poza tymi pryncypiami pomysły zawierały jednak trudne do zignorowania różnice. Przykładowo teoria typu I przypisywała istotną rolę strunom otwartym o swobodnych krańcach, podczas gdy pozostałe preferowały przypominające pętle, struny zamknięte. Pierwsza teoria heterotyczna korzystała z symetrii oferowanej przez specjalną grupę ortogonalną SO(32), a druga została oparta o grupę Liego E8. I tak dalej.
W tych okolicznościach teoria strun zaczęła po raz kolejny budzić uzasadniony sceptycyzm. Koncepcja mająca unifikować reguły rządzące wszechświatem, nagle sama uległa rozbiciu i potrzebowała ujednolicenia. Zamiast uzyskania obiecanej arcyodpowiedzi, na wierzch zaczęły wypływać nowe pytania. Pomyśl o tym przez chwilę. Czy ten sam kosmos może być opisywany równie prawidłowo przez kilka odmiennych zestawów reguł? Czy to nie dziwne? A może każdy z pięciu wariantów wygląda z wierzchu na pasujący, ale w rzeczywistości prawidłowy jest tylko jeden z nich?
W tym drugim przypadku sytuacja przypominałaby nieco kwestię opisu oddziaływania grawitacyjnego. Prawa sformułowane przed wiekami przez Izaaka Newtona wciąż pozwalają na dokładne wyjaśnienie ruchu ciał niebieskich czy słanie rakiet do wyznaczonego celu; podobnie do równań ogólnej teorii względności Alberta Einsteina – a przecież obie koncepcje pozostają znacząco różne. Sęk w tym, że choć prace obu geniuszów rzeczywiście rozwiązują bliźniacze problemy i opisują ten sam skrawek przyrody, to fizyka newtonowska sprawdza się tylko w pewnym przybliżeniu, w niektórych przypadkach zwyczajnie zawodząc. Dlatego teoretycy mają swoje powody, aby nie ufać teoriom sprawdzającym się rzekomo równie dobrze, w wielu odmiennych wariantach. Naturalne staje się podejrzenie, że tylko jedna z propozycji zbliża nas do zrozumienia mechanizmu wszechświata. Albo żadna.

Struny ’95
Fizyka, jako nauka ścisła, bardzo nie lubi takich dylematów. Teoria strun już raz wylądowała na śmietniku i uniknęła zapomnienia tylko dzięki zapalczywości Schwarza i Greena. Z kolejną odsieczą przybył jej matematyk Instytutu Badań Zaawansowanych w Princeton, Edward Witten (na zdjęciu). Genialny umysł, już wtedy laureat Medalu Fieldsa i wybitny ekspert w tematach wielowymiarowej geometrii oraz supersymetrii – krótko mówiąc, idealny kandydat na superbohatera, który rozsupła bolączki teorii strun.
Ed Witten swój gorący romans z fizyką rozpoczął w Los Angeles, podczas błyskotliwego wykładu w ramach konferencji Struny ’95. Przyszłość i perspektywy. Kalifornijskie aule gościły wtedy wiele znaczących figur: Johna Schwarza, Michaela Greena, Briana Greenego (proszę, nie myl tych panów), Davida Grossa, czy Josepha Polschinskiego. Mało kto spodziewał się, że show tym wybitnym fizykom skradnie matematyk. Jak wspomina Leonard Susskind: “Rzekł kilka słów, które mnie zainteresowały, po czym przez resztę wykładu byłem wciąż zaaferowany początkiem jego wypowiedzi i kompletnie zgubiłem sens dalszego wystąpienia”. Pewnie zastanawiasz się, w jaki sposób prelegent tak głęboko wstrząsnął zgromadzonymi na widowni uczonymi?
W godzinnym wywodzie, pod hasłem Niektóre uwagi o dynamice strun, Witten stwierdził, że nie ma najmniejszego powodu, aby skreślać którąkolwiek z opracowywanych wersji budowanej teorii. Przeciwnie, dowiódł, iż wszystkie 10-wymiarowe teorie strun stanowią tak naprawdę przybliżenia wyższej, bardziej tajemniczej, 11-wymiarowej teorii. Już nieco wcześniej pojawiło się kilku badaczy potrafiących wykazać pewne powinowactwa – czy też mówiąc mądrzej, dualności – między teorią typu IIA i typu IIB lub między typami heterotycznymi SO(32) i E8. Profesor Princeton wykazał jednak znacznie więcej.
Każde przewidywanie, odpowiednio zinterpretowane matematycznie, sprawdziło się. I nie było to z jakiegoś powodu pojęciowego. Nie wiemy dlaczego się sprawdzają, po prostu liczymy osobno obie strony równania i faktycznie uzyskujemy te same struktury, symetrie i wyniki. Dla matematyka tego typu rzecz nie może być przypadkiem, musi istnieć jakaś głębsza przyczyna.
Richard Thomas
Jego zdaniem, jeżeli weźmiemy w rachubę geometrię 11-wymiarową i zwiniemy odpowiedni wymiar, przekształci się ona w któryś z poznanych pięciu typów teorii strun. Mówiąc najprościej, każdy z rodzajów strun to nic innego, aniżeli okrojone odbicie tej samej, głębszej całości. Tak powstała nowa, uogólniona teoria strun, pozostająca do chwili obecnej głównym obiektem westchnień fizyków poszukujących klucza do wielkiej unifikacji. Witten nadał swojemu projektowi nazwę M-Teorii.
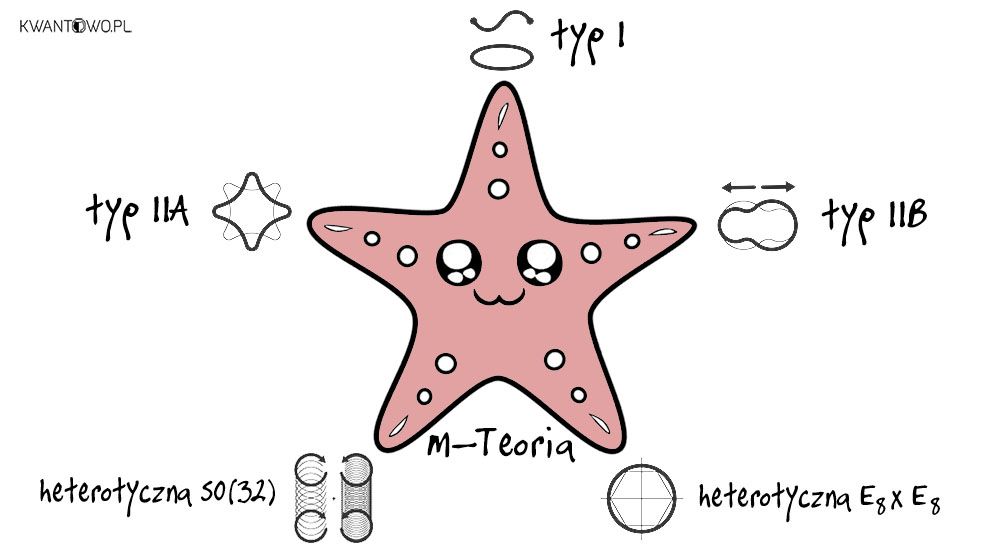
Zapytasz co w M-Teorii oznacza “M”? Trzeba przyznać, że Edward Witten nie tylko ukuł elegancką koncepcję, ale również zadbał o odpowiednio enigmatyczną i intrygującą nazwę. Otóż nie ma pewnej odpowiedzi na to pytanie, a wersji jest tyle, ilu fizyków zajmujących się strunami. Magiczna teoria, mistyczna teoria, monstrualna teoria, teoria-matka… Do wyboru do koloru. Jednak najczęściej mówi się o teorii macierzowej lub tajemniczej teorii (ang. mysterious theory). Mnie z kolei najbardziej trafiło do gustu wyjaśnienie humorystyczne, stwierdzające, że Witten planował ochrzcić swoje dziecko W-Teorią, lecz z uwagi na wrodzoną skromność wywrócił “W” do góry nogami.
Matka wszystkich teorii
Źródłem potęgi M-teorii, podobnie jak wcześniejszych teorii strun, są dodatkowe wymiary przestrzenne. Jak wiesz z poprzedniej części cyklu, pomysł unifikacji oddziaływań poprzez założenie istnienia nowych wymiarów nie był nowy, jednak jego zwolennicy postulowali zupełnie różne liczby. Na pewnym, wczesnym etapie struny miały sprawować się najlepiej w 26 wymiarach. Później, uwzględniając osiągnięcia supersymetrii, postawiono na formalizm 10-wymiarowy, wykorzystywany przez pięć wspomnianych na początku wersji teorii strun. Zdaniem Edwarda Wittena, równania jego kolegów wręcz prosiły się o jeszcze jeden stopień swobody, który automatycznie objawiłby ich pokrewieństwo.
Co my tu właściwie mamy? 11 wymiarów oznacza istnienie 3 znanych nam wymiarów przestrzennych (tył-przód, lewo-prawo, góra-dół), 1 wymiaru czasowego, oraz 7 pozwijanych, egzotycznych wymiarów, niedostępnych dla naszych zmysłów. Owe zwijanie należy tu traktować dość dosłownie, choć niełatwo to zobrazować.
Liczę na to, że pamiętasz popularny eksperyment myślowy z dwuwymiarową krainą płaszczaków. Nie rozumieliby oni, czym jest trzeci wymiar przestrzenny, a ich rzeczywistość wyglądałaby z naszej perspektywy jak kartka papieru. Gdybyśmy tę kartkę zwinęli w rulon i nałożyli gumkę, to biedny płaszczak-podróżnik maszerując przed siebie ciągle wracałby do punktu wyjścia. Pójdźmy o krok dalej i spróbujmy zwinąć papierową rurkę najmocniej, jak tylko potrafimy. Patrząc na otrzymany obiekt z daleka, zobaczymy już tylko jednowymiarowy odcinek, o pewnej długości, ale pozbawiony szerokości i głębokości. Dopiero bliższe oględziny ujawnią prawdziwe oblicze tej struktury.
Niestety w przypadku omawianych teorii sprawa jest dalece bardziej skomplikowana, bo nie dość, że mowa o kilku wymiarach zupełnie obcych ludzkiemu umysłowi, to jeszcze wielowymiarowe struny pozostają zdecydowanie zbyt małe by zarejestrować je jakąkolwiek aparaturą. Jednak w tym szaleństwie jest metoda, bowiem nowe wymiary są równoznaczne z większą liczbą kierunków w jakim drgają struny. Z kolei sposób drgania decyduje o charakterystyce fizycznej danego obiektu – od jego masy, po ładunek elektryczny. A co w tym wszystkim robi jedenasty wymiar M-Teorii? Witten potraktował mikroskopijne wymiary pięciu teorii strun podobnie do pięciu złożonych na różny sposób kartek papieru. Rozwinął je w wyższym wymiarze, pokazując, że w istocie są dokładnie tą samą strukturą.
Dodatek: Dziwaczne kształty Calabiego-Yau
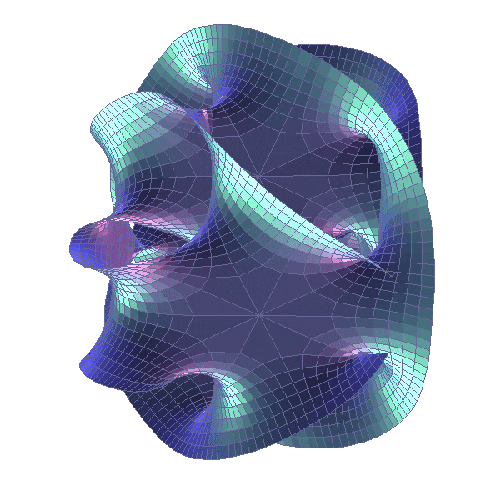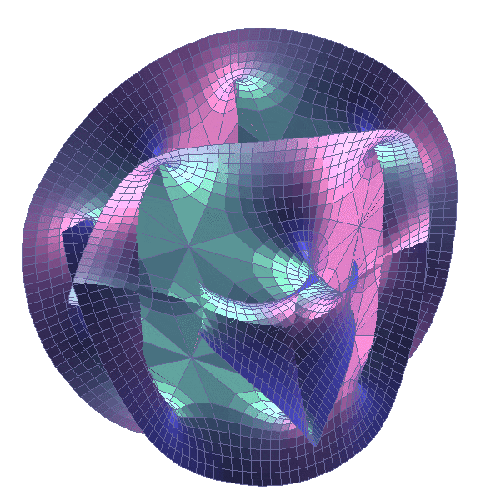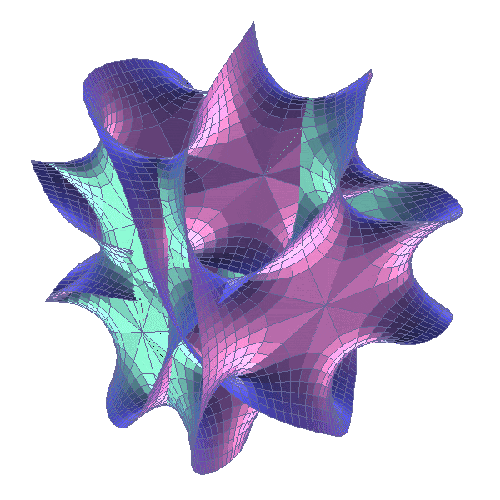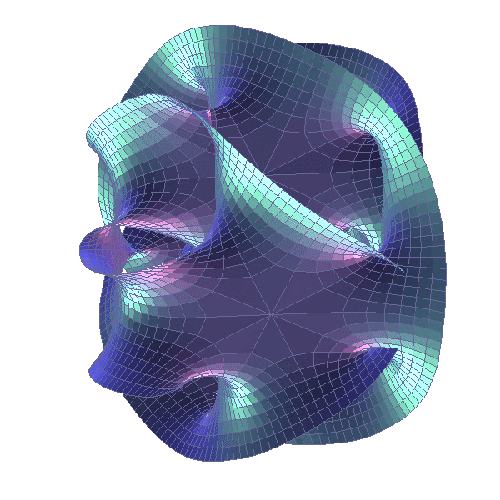
Od strony matematycznej M-Teoria należy do najbardziej zawiłych koncepcji w całej fizyce. Zwinięte wymiary opisuje się na bazie rozmaitości sformułowanych niezależnie od teorii strun przez Eugenio Calabiego z Uniwersytetu Pensylwanii oraz Shing-Tunga Yau z Uniwersytetu Harvarda. Mogłeś widzieć artystyczne przedstawienia tych wielowymiarowych struktur, nawet nie zdając sobie z tego sprawy – ponieważ bardzo często zdobią wszelkie artykuły dotyczące teorii strun. Naturalnie musimy przy tym mieć świadomość, że dwuwymiarowy obraz nigdy nie odda subtelności tak zwariowanej geometrii. Poza tym, przestrzenie Calabiego-Yau występują w bardzo wielu wersjach, wykorzystywanych przez fizyków na różne sposoby. Łączy je właściwie tylko liczba wymiarów oraz możność zastosowania symetrii lustrzanej, pozwalającej przekształcać jeden kształt Calabiego-Yau w inny.
W każdym razie, teoria strun zakłada, że wszechświat pozostaje wypełniony wszechobecnymi, zwiniętymi do najmniejszych rozmiarów przestrzeniami Calabiego-Yau. W tym momencie wszędzie wokół Ciebie, a nawet w Tobie, znajduje się niezliczona ilość tych mikroskopijnych zawijasów.
Kolejnym darem Eda Wittena i jego teorii było wprowadzenie do gry całkiem nowych zawodników – membran. W literaturze częściej jednak spotkasz nazwę bran lub p-bran, gdyż membrany przywodzą skojarzenia z dwuwymiarowymi przegrodami lub błonami, zaś M-Teoria, obok oswojonych krzywych i pętelek, przewiduje istnienie całej gamy różnowymiarowych struktur (2-brany, 3-brany, 4-brany itd.). W istocie, brany były obecne w teorii strun cały czas, lecz bez jedenastego wymiaru naukowcy dopatrywali się najwyżej ich niepełnych odcisków. Podobnie jak hipotetyczny płaszczak widziałby jedynie przekrój naszego palucha, którym wkroczylibyśmy do jego dwuwymiarowego podwórka.
W ten sposób do talerza fizycznego spaghetti wrzucono nam całą garść cannelloni, lumache i innych zdeformowanych klusek.
M-Teoria = M-Kosmologia
Potencjalna teoria wszystkiego ma w pierwszej kolejności odnaleźć wspólny mianownik dla mechaniki kwantowej i grawitacji. Przyznasz jednak, że byłoby miło, gdyby zawierała też pewne przewidywania dotyczące wszechświata jako całości. I rzeczywiście, znaleźli się naukowcy, którzy podjęli próbę wytłumaczenia na gruncie strun takich – zdawałoby się bardzo odległych zagadnień – jak entropia czarnych dziur, przyszłość kosmosu czy sam wielki wybuch. Poteoretyzujmy więc na koniec o tym co oferują struny w skali kosmologicznej.

Mówiliśmy wcześniej o tym, jak można by zwinąć dwuwymiarowy świat płaszczaków. Być może zaświtała Ci wtedy myśl, czy podobna rzecz nie mogłaby dotyczyć naszej czasoprzestrzeni. W istocie, część teoretyków bierze pod uwagę scenariusz, zgodnie z którym istnieją nie tylko nieznane wymiary o rozmiarach subatomowych, ale również pewna hiperprzestrzeń, wewnątrz której uwięziony pozostaje znany nam wszechświat. Podobne idee pojawiały się już wcześniej, ale M-Teoria daje im nowe, całkiem solidne fundamenty. Szczególnie dobrze w świecie strun czują się entuzjaści wszechświata ekpyrotycznego, powstałego w wyniku wielkiej kraksy. Kiedy piszę wielkiej, mam na myśli naprawdę ogromną kolizję, z udziałem dwóch… wszechświatów. Taka opcja mogłaby się zadziać, gdyby cała otaczająca nas czasoprzestrzeń – traktowana jako ogromna brana – zetknęła się z podobnym tworem, w pięciowymiarowej hiperprzestrzeni, zwanej czasem objętością obejmującą.
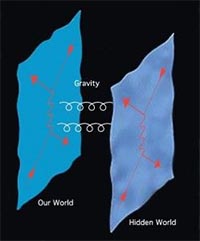
Gdyby kosmos był dwuwymiarową płaszczyzną, to olbrzymie brany wyglądałyby jak równoległe do siebie, zawieszone w przestrzeni kartki papieru. Jeśli kartki się zetkną dochodzi do monstrualnej erupcji energii, dostatecznie dużej aby po ostudzeniu utworzyła niezliczone ilości galaktyk, gwiazd, czarnych dziur i planet. W tym modelu nigdy nie było osobliwości przewidywanej przez standardowe wersje wielkiego wybuchu, a obecna charakterystyka wszechświata (warunki brzegowe) wynikałaby ze sposobu i energii wielkiej kolizji bran. To co stało się później nie powinno natomiast różnić się od tego co wiemy i co opisuje klasyczna kosmologia. Co ciekawe, idea multiwersum tłumaczyłaby dlaczego grawitacja wydaje się beznadziejnie słaba, w porównaniu do pozostałych oddziaływań. Otóż przyciąganie grawitacyjne jako jedyne nie byłoby zatrzaśnięte w naszej branie, oddziałując również w hiperprzestrzeni. W związku z tym odczuwamy jedynie ułamek jego rzeczywistej siły, podczas gdy reszta wycieka na zewnątrz naszego wszechświata. Jest zdecydowanie za wcześnie aby traktować taki koncept jako prawdopodobny, ale bez wątpienia dostarczyłby naukowcom wiele kuszących rozwiązań. Kto wie, czy np. anomalie grawitacyjne tłumaczone obecnie obecnością ciemnej materii, nie zostałyby uznane za przyciąganie masy leżącej w innej kosmicznej branie. Nasze galaktyki formowałyby się w miejscach sąsiadujących ze skupiskami materii w innym wszechświecie, wzajemnie usztywniając swoje struktury.
Na dokładniejsze opracowanie czeka tu całe mnóstwo pytań. Co z czasem? Czy w pięciowymiarowej nadprzestrzeni zegary tykają podobnie do tych naszych? Czy forma naszej czasoprzestrzeni została ustalona podczas kraksy, czy była zdefiniowana już wcześniej? Ile istnieje kosmicznych bran? Czy do ich zderzeń dochodzi w związku z przyciąganiem grawitacyjnym, fluktuacjami kwantowymi, czy jeszcze z innego powodu? Czy w przyszłości dojdzie do kolejnych kolizji, przypominających tę sprzed 13,82 miliardów lat? Musimy zachować sceptycyzm i pamiętać, że to tylko jedna z kilku, jeżeli nie kilkunastu propozycji, wciąż raczkującej kosmologii branowej. Odpowiedzi na wszystkie palące kwestie możemy uzyskać za dekady, stulecia lub nigdy.
Niekoniecznie zakończenie
Unifikacja praw przyrody to moim zdaniem najtrudniejsze, największe, ale i najbardziej wyrafinowane wyzwanie z jakim przyszło zmierzyć się ludzkiemu intelektowi. Nie mamy pojęcia czy M-Teoria nie wiedzie nas na manowce i jeszcze przez wiele lat na pewno się tego nie dowiemy. Jednak nawet jeśli teoretycy strun trafili matematyczną kulą w płot, trudno nie chylić czoła przed ukutym przez nich formalizmem oraz przed ideą wszechświata dogłębnie symetrycznego, jednolitego i po prostu eleganckiego. Pewny jestem jednego: współczesna fizyka jak tlenu potrzebuje nowej, potężnej teorii. Tylko w ten sposób otworzymy furtkę do setek rewolucyjnych odkryć zdających się dzisiaj fantastyką lub leżących aktualnie poza naszą wyobraźnią.
Oponenci psioczą, że ludzkość nie jest zdolna do udowodnienia istnienia strun, zatem nie mamy do czynienia z prawdziwą nauką. Z tego powodu dla wielu to mrzonki, bajki, a w najlepszym przypadku nieweryfikowalna filozofia. Nie przeczę: to gigantyczny problem. Wierzę jednak, że umysł ludzki pokona i tę przeciwność, jeśli nie teraz to w dalekiej przyszłości. A co jeśli eksperymenty udowodnią błędność torii strun? Niewątpliwie byłby to cios dla całej rzeszy świetnych naukowców, którzy poświęcili swoje kariery na badania nad nią. Myślę jednak, że ich wysiłek nie pójdzie na marne, a po wiekach dopasowywania do siebie elementów kosmicznej układanki, z naukowego zamętu wyłoni się teoria wszystkiego.
Tymi oto słowami kończę pięcioodcinkowy cykl Kosmiczna symfonia. Doskonale zdaję sobie sprawę, iż nie poruszyłem wszystkich zagadnień, a te poruszone zawierają całe mnóstwo interesujących zakamarków. Jednak moim celem było przede wszystkim stworzenie czytelnego opracowania, które pozwoli czytelnikowi uzyskać wgląd w podstawowy cel przyświecający pracom fizyków. Mam nadzieję, że uczyniłem słusznie i kilka osób zainteresowałem tematem. Powiedzmy sobie szczerze: cóż może być ciekawszego od próby złamania kodu wszechświata?
Poprzednie części cyklu:
Kosmiczna symfonia cz.1: Teoria wszystkiego;
Kosmiczna symfonia cz.2: Od kwantu do struny;
Kosmiczna symfonia cz.3: Teoria strun;
Kosmiczna symfonia cz.4: Supersymetria.