Materia nie odgrywa już głównej roli w fizyce. Jej miejsce zajęły zasady symetrii, z których pewne w obecnym stanie wszechświata pozostają ukryte.
Steven Weinberg
Przyroda żąda symetrii
Na początku muszę Cię uprzedzić, że wkraczamy w najbardziej niegościnny – przynajmniej z punktu widzenia nie-fizyków – etap naszej opowieści o unifikacji praw natury. Nie oddalimy się zanadto od omawianych już zagadnień teorii względności, mechaniki kwantowej oraz modelu standardowego; jednakże spojrzymy na nie od innej strony. Mianowicie, interesować nas będzie perspektywa symetrii. To kłopotliwe o tyle, iż symetria (a co dopiero supersymetria!) w fizyce cząstek elementarnych przerasta pospolity sens tego słowa. Spoczywa na fundamencie zupełnej abstrakcji, niemal nieuchwytnej dla naszych zmysłów i wyobraźni. Trochę to ironiczne, bo przecież w znaczeniu, jakim posługujemy się nią na co dzień, nie wydaje się czymś skomplikowanym. Kojarzy się z geometrią, barwną i łatwą do zobrazowania. W każdym razie przyrzekam, że zrobię co w mojej mocy, aby przeprowadzić Cię przez to zagadnienie w miarę bezboleśnie, jednocześnie pozwalając Ci poczuć siłę jego wyjątkowości. A jest naprawdę wyjątkowe.

Zatrzymajmy się na razie przy podejściu intuicyjnym i geometrycznym. Pomyśl o stokrotce, jaką możesz znaleźć na trawniku. Zakładając, że nie jest zbyt obszarpana, przez jej krągły kwiat możesz przeprowadzić całe mnóstwo linii prostych w taki sposób, aby obie połówki wyglądały tak samo. Możesz też obracać kwiat w ręce i cieszyć się faktem, iż wygląda tak samo bez względu na kąt obrotu. Symetrię zdefiniujemy zatem jako możność poddania obiektu takiej operacji, po której będzie wyglądał on tak samo. Jeszcze krótsze wyjaśnienie brzmi: symetria to zmiana bez zmiany. Gdybyś wyrwał któryś z płatków, kwiat będzie wyglądał dla Ciebie tak samo, ale dopiero po zatoczeniu pełnego koła, czyli 360 stopni. Zauważ, iż zarówno w tym przypadku jak i w innych, do których zaraz przejdziemy, chodzi tak naprawdę o pewne metody przekształcenia obiektu. Chcąc dorysować obok jakiejś figury drugą, symetryczną, w istocie szkicujemy jej odwrócone lustrzane odbicie. To już jakiś rodzaj przekształcenia figury w przestrzeni.
Bardziej zaawansowaną transformacją będzie np. anamorfoza, polegająca wręcz na zdeformowaniu przerysowywanego ciała, trochę jak w krzywym zwierciadle. Znając zasady, według których dokonano anamorfozy, możliwym jest “naprostowanie” karykaturalnego obrazu i odzyskanie pełnego oryginału. Za przykład mogą posłużyć transformacje wykorzystywane podczas sporządzania map. Chcąc nanieść obraz kuli ziemskiej na płaszczyznę, kartografowie często tworzą złudzenie poszerzania się terytoriów w kierunku biegunów. Dlatego przeglądając atlas ulegamy złudzeniu, że np. Polska ma podobne rozmiary do Nigerii czy Kolumbii, podczas gdy w rzeczywistości oba kraje mają trzykrotnie większą powierzchnię.
Symetria sił i praw zachowania
Współcześni fizycy mają prawdziwego hopla na punkcie symetrii. Głównie dlatego, że zdaje się ona wynikać z najgłębszych reguł rządzących rzeczywistością. Wystarczy rozejrzeć się dookoła, aby dostrzec, iż przyroda usilnie premiuje symetrię (nawet jeśli nie zawsze chodzi o prostą symetrię osiową albo obrotową jak przy stokrotce), a my jesteśmy wręcz zaprogramowani, aby tę estetykę doceniać. A skoro dostrzegamy ją w całym świecie makroskopowym, mamy przesłankę, żeby doszukiwać się jej śladów również u samych podstaw. Tylko jak manifestuje się symetria w przypadku cząstek, oddziaływań i praw fizyki?

Weźmy za przykład grawitację. Niezależnie od tego, czy znajdujemy się w pomieszczeniu, czy na zewnątrz, czy jesteśmy obróceni w lewo, czy w prawo, czy dokonamy pomiaru dzisiaj, czy w roku 2101 – Ziemia będzie nas przyciągać dokładnie w ten sam sposób. Co więcej, możesz mi wierzyć na słowo, że siła ciążenia prezentuje się identycznie w każdym zakątku wszechświata. Oczywiście masywniejsze ciało będzie nas przyciągać mocniej niż to mniejsze, ale dzieje się to na gruncie twardego i niezmiennego wzoru. Gdybyśmy więc posiadali boską moc przesunięcia wszystkich galaktyk, gwiazd i układów planetarnych (ogólnie wszystkiego co posiada jakąkolwiek masę) dokładnie o rok świetlny w tym samym kierunku, nie zauważylibyśmy absolutnie żadnej różnicy. Jeśli znów chwycimy wszystkie galaktyki, gwiazdy i układy planetarne, obracając całą zawartość wszechświata np. o 90 stopni, również nie groziłyby nam żadne reperkusje.
Rzecz zdawałoby się oczywista, a jednak intrygowała najtęższe umysły, począwszy od Galileusza, kończąc na Einsteinie. Ten ostatni uczynił nawet z tej myśli podstawę i pierwszy postulat swej szczególnej teorii względności (rozszerzony później na układy nieinercjalne w ogólnej teorii względności). Dało nam to elegancką czasoprzestrzeń, w której każdy obserwator cieszy się dokładnie takimi samymi prawami fizyki oraz pełnym równouprawnieniem. Gdybyś wylądował teraz w jakimś bezgwiezdnym zakamarku kosmosu, nie byłbyś nawet w stanie stwierdzić czy spoczywasz w miejscu, czy może posuwasz się z zawrotną prędkością. A jeśli przypadkiem minąłbyś drugiego nieszczęśnika – wiele Ci to nie pomoże, ponieważ obaj macie takie samo prawo uważać się za tych nieruchomych. A do tego wszystkiego dochodzi einsteinowskie stwierdzenie, na mocy którego, dla was i każdego innego obserwatora, bez względu na jego ruch, prędkość światła w próżni ma stałą i niezmienną wartość.
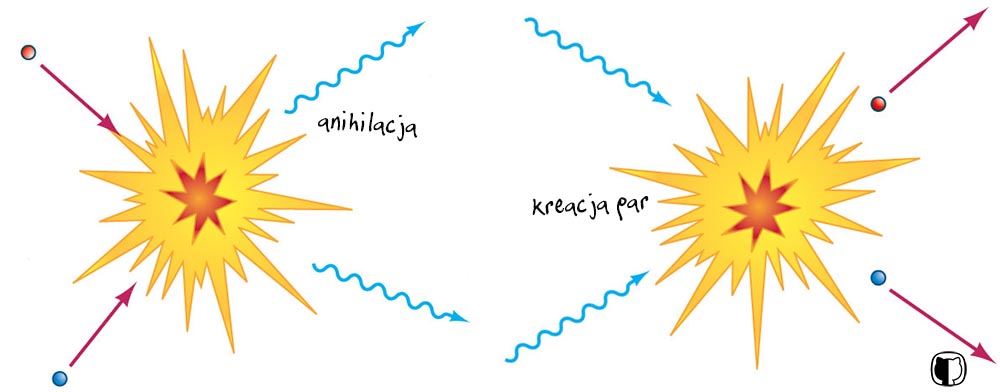
Czy nie zgubiliśmy gdzieś po drodze tematu symetrii? Nic z tych rzeczy. Tak naprawdę właśnie podziwialiśmy symetryczny charakter przestrzeni, w której możemy dokonywać wielu zmian bez zmiany. Pójdźmy jednak o krok dalej. Jak na pewno wiesz, w fizyce istnieją pewne niezmienne wielkości, których najzwyczajniej w świecie nie da się stworzyć czy zlikwidować. Mówimy o prawach zachowania energii, ładunku elektrycznego, pędu czy momentu pędu. Choć to zaskakujące, np. fundamentalna zasada zachowania energii wynika wprost z symetrii w czasie! Energii nie można stworzyć ani usunąć, lecz co najwyżej przekazać bądź przekształcić. Kiedy elektron spotka pozyton (czyli swoją antycząstkę), niechybnie dojdzie do wzajemnej anihilacji i przekształcenia masy obu drobin w konkretną porcję energii. Gdyby nie funkcjonowała symetria w czasie, moglibyśmy się zastanawiać, czy aby anihilacja nie wyzwoli nienaturalnie wielkiej energii lub czy obie cząstki nie znikną z tego świata, nie pozostawiając po sobie śladu. Takie rzeczy się jednak nie zdarzają, a symetria w czasie gwarantuje, że energia nie wycieka nam nigdzie poza wszechświat. W dodatku proces anihilacji jest symetrycznie odwracalny – gdyż wysokoenergetyczne promieniowanie gamma ma potencjał, żeby wykreować parę elektron-pozyton.
A skoro już jesteśmy przy antymaterii, to na jej przykładzie możemy również podziwiać rewelacyjne funkcjonowanie zasady zachowania ładunku. Wysoka energia może doprowadzić do kreacji materii, ale nigdy nie uświadczymy narodzin pojedynczego elektronu ani pojedynczego pozytonu. Zawsze powstaje para o przeciwnych ładunkach elektrycznych, ponieważ koniec końców bilans musi wyjść na zero. To naprawdę dosadna ilustracja niezachwianej dominacji symetrii w przyrodzie.
Tak na marginesie. Wiekopomne dzieło skojarzenia praw zachowania z regułami symetrii, zawdzięczamy żyjącej na początku ubiegłego stulecia matematyczce Emmy Noether. Czuję się w obowiązku to podkreślić, gdyż mamy tu do czynienia z doprawdy genialnym umysłem, zdecydowanie zbyt łatwo pomijanym w popularnych opracowaniach.
Symetria jest po to żeby ją łamać
Jak powiedzieliśmy, symetria daje nam poczucie fizycznego egalitaryzmu. W każdym miejscu, każdego obserwatora obowiązują dokładnie te same prawa. Prawda? W zasadzie tak, ale jednak nie do końca. Grawitacja przyciąga każdy obiekt wyposażony w masę zgodnie z pewnym wzorem. Elektromagnetyzm analogicznie pozwala na interakcję między ciałami legitymującymi się ładunkiem elektrycznym. Jesteśmy do tego stanu rzeczy tak przyzwyczajeni, że rzadko zastanawiamy się, dlaczego w ogóle poszczególne oddziaływania funkcjonują i dlaczego akurat w taki sposób? Przecież moglibyśmy wyobrazić sobie rzeczywistość, w której każda cząstka posiada dokładnie takie same właściwości, reagując identycznie na każde z czterech oddziaływań podstawowych. Albo jeszcze lepiej, w której funkcjonuje tylko jedno oddziaływanie i tylko jeden rodzaj cząstek o bliźniaczych cechach. Jakaż to byłaby symetria!
Wiele wskazuje na to, że taki stan rzeczy cechował wszechświat zaraz po wielkim wybuchu, w pierwszym ułamku sekundy. Grawitacja, oddziaływanie silne, elektromagnetyzm i oddziaływanie słabe stanowiły jedność i wraz z szybkim rozrzedzaniem energii kolejno ulegały wyodrębnianiu. U zarania wszystkie drobiny musiały więc pozostawać kompletnie nierozróżnialne. Potem nastąpiły tąpnięcia skutkujące złamaniem symetrii. Łatwo to zrozumieć na przykładzie jednego z najbardziej brzemiennych pęknięć, jakie nastąpiło za sprawą popularnego bozonu Higgsa. Wyobraź sobie wszechświat pozbawiony pojęcia masy. Wszystkie cząstki zachowują się bardzo podobnie i niczym foton mogą wesoło hasać w przestrzeni z prędkością światła. Wtedy wkracza podstępny higgson i burzy ten sielski (o ile rozpaloną do miliardów kelwinów niestabilną przestrzeń można określić jako sielską) krajobraz, nadając wszystkim obiektom nową cechę, która już na zawsze będzie je różnicować.
Załóżmy, że widoczne na ilustracji biedronki symbolizują cząstkę pozostawioną na pastwę złamania symetrii. Chociaż w każdym z trzech przypadków biedronka pozostaje biedronką, przewrócona o jakiś kąt może nas zmylić. Oczywiście rzeczywistość jest znacznie bardziej skomplikowana, ale skutki zburzenia pierwotnej estetyki sprowadzają się do tego samego. Nagle wśród identycznych cząstek o ładunku -1 i spinie 1/2 nastąpił wyraźny rozłam. Pojawiła się nowa właściwość – masa – która wyodrębniła lekkie elektrony, masywniejsze miony i tłuste taony. Gdybyśmy wyłączyli pole Higgsa, wszystkie biedronki wróciłyby do naturalnej pozycji, zaś elektron, mion i taon znów byłyby nierozróżnialne. Wyłączając dodatkowo pole elektromagnetyczne oraz pole Yanga-Millsa (związane z oddziaływaniami jądrowymi) zniknęłyby również pozostałe podziały, przywracając światu zapomnianą elegancję.
Fizycy podejrzewają, że owa pierwotna symetria panująca u zarania czasu wciąż jest odczuwalna, chociaż leży w ukryciu i ujawni się dopiero po zastosowaniu właściwego przekształcenia. Właśnie do tego dąży nauka – do dostatecznie mocnego kopnięcia biedronki. Dokonując odpowiednich operacji, pragniemy wykazać, iż foton jest zdeformowanym odbiciem bozonów W i Z, a te z kolei, pozostają odbiciem gluonów. Jeśli pamiętasz drugą część tego cyklu, to wiesz, że część tego planu doczekała się już realizacji. Eksperymentatorzy w latach 80. pokazali jak przy olbrzymich energiach bozony W i Z zaczynają przypominać fotony, odsłaniając tożsamość oddziaływania słabego oraz elektromagnetycznego. Kolejne generacje akceleratorów cząstek elementarnych, dysponujące większą mocą niż obecne, pozwolą nam jeszcze lepiej odwzorować warunki wielkiego wybuchu i być może zweryfikować kolejne postacie symetrii.
Mała matematyczna dygresja
Językiem służącym wdrażaniu reguł symetrii w koncepcje fizyczne jest teoria grup, podwędzona od norweskiego matematyka Sophusa Liego. Tak jak pisałem w drugiej części cyklu, na początku lat 80. Adbus Salam, Sheldon Glashow oraz Steven Weinberg postawili dwa istotne kroki prowadzące do unifikacji oddziaływań podstawowych. Nie napisałem wtedy jednak, iż dla osiągnięcia celu, nobliści zaadoptowali liczące ponad sto lat zasady symetrii Liego. Na fali modelu standardowego szanowane periodyki rychło wypełniły się wymyślnymi typami symetrii, jak: SU(n+1), SO(2n+1), SP(2n), E(6), E(8). Litery obecne w tych oznaczeniach bynajmniej nie są przypadkowe. “U” oznacza unitarność, a więc zachowanie wektorów w płaszczyźnie zespolonej. Od “O” zaczyna się określenie ortogonalny, czyli związany z grupą obrotów. “S” to specjalny, co w tym kontekście oznacza brak odbić. “E” pochodzi natomiast od angielskiego exceptional (wyjątkowy). I tak dla przykładu, Salam, Glashow i Weinberg projektując teorię oddziaływań elektrosłabych użyli matematycznej symetrii SU(2)xU(1). Wkrótce potem spróbowali zastosować symetrię SU(5) do włączenia w to wszystko gluonów i w rezultacie wyprowadzenia teorii wielkiej unifikacji, GUT. Możliwe, że niewiele z tego wszystkiego rozumiesz. Niestety akurat w tym przypadku wysmarowanie jakiejś barwnej metafory graniczy z cudem i trudno powiedzieć coś więcej bez uciekania się do karkołomnych modeli matematycznych. Mimo wszystko myślę, że warto przynajmniej usłyszeć o narzędziach, którymi tęgie umysły świata rzeźbią swoje dzieła.
Drużyny fermionów i bozonów
Powoli, ale pewnym krokiem zbliżamy się w kierunku tytułowej supersymetrii. Jednak zanim dotrzemy do celu, musimy uzupełnić kilka informacji na temat podstaw fizyki mikroświata (z góry przepraszam stałych czytelników i innych wyjadaczy). Konkretniej interesować będą nas konsekwencje wynikające z pewnej cechy cząstek elementarnych, którą dość powszechnie wiąże się z momentem pędu.
Nie będziemy za wiele dywagować o samym spinie (z ang. wirować, obracać) i jego naturze, gdyż nie jest to szczególnie istotne dla dalszej narracji. Czuję się jednak zobligowany, żeby zwrócić Ci uwagę, że wbrew wszystkiemu, co zobaczysz w sieci, u Hawkinga, u Greenego, u Kaku czy nawet u mnie – cząstki elementarnej nie da się w zadowalający sposób przyrównać do żadnego ciała znanego z naszych codziennych doświadczeń. W Krótkiej historii czasu przeczytasz, iż elektron rotuje wokół własnej osi niczym puszczony w ruch bączek. Na nasze skromne potrzeby taki obraz spinu wydaje się wystarczający, ale pamiętaj: nie oddaje on do końca specyfiki kwantowych zjawisk. Spin z wirowaniem łączy właściwie tylko to, że dany elektron zdaje się regularnie wracać do punktu wyjścia, tak jak kręcące się wokół własnej osi ciało. Do tej analogii nie pasuje natomiast to, jak ten obrót wygląda. Kiedy namalujesz na bączku kropkę, musisz dokonać obrotu obiektu o pełne 360 stopni, aby znów ujrzeć to samo. Fizyk cząstek przypisałby takiej zabawce spin równy 1. Niesforny elektron musi natomiast wykonać obrót o… 720 stopni – czyli przekręcić się wokół własnej osi dwukrotnie – aby wrócić do punktu wyjścia. Taki spin ma wartość wyrażaną ułamkiem 1/2. Tak, to bardzo nieintuicyjny stan rzeczy, ale jak wspomniałem, nie powinieneś się tym teraz przejmować.
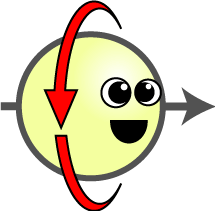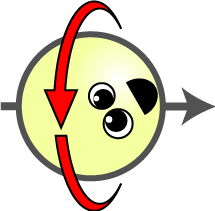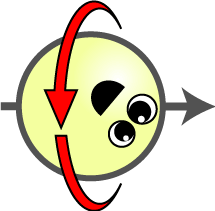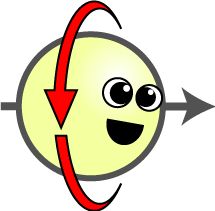
Interesuje nas fakt, iż spin pozostaje jednym z podstawowych przymiotów każdej cząstki elementarnej (jedną z liczb kwantowych) i dzieli je na dwie arcyważne rodziny. Pierwsza nosi dumną nazwę fermionów, odziedziczoną po nobliście i wynalazcy pierwszego reaktora jądrowego, Enricu Fermim. Druga to bozony, ochrzczone ku pamięci Satyendry Bosego, hinduskiego fizyka blisko współpracującego z Einsteinem, z którym opracował statystykę Bosego-Einsteina oraz koncepcję kondensatu Bosego-Einsteina. Zasada podziału jest dość prosta i brzmi następująco: każda cząstka o spinie wyrażonym liczbą całkowitą przynależy do kategorii bozonów; zaś każdą drobinę o spinie połówkowym przyporządkowujemy do fermionów. Istnieją też bardziej namacalne różnice. Otóż fermiony podlegają zakazowi Pauliego, tj. nie bardzo lubią przebywać w tym samym miejscu w tym samym czasie (a dokładniej nie mogą w ogóle przebywać w tym samym stanie kwantowym). I tak, nieprzenikliwe fermiony – zwłaszcza elektrony i kwarki – stanowią niezbędny budulec całej otaczającej nas materii. Bozony nie podlegają regule Pauliego i odpowiadają za przenoszenie wszystkich fizycznych oddziaływań. Należą do nich rzecz jasna wspomniane już fotony, gluony, wuony czy zetony, o spinie równym 1. Nie możemy też zapomnieć o bozonie Higgsa, choć ten postawił na oryginalność i jako jedyny z kwantowych kurierów posiada spin zerowy. Dla porządku wymieńmy też wciąż niezaobserwowany grawiton, zgodnie z założeniami teoretyków noszący spin równy 2.
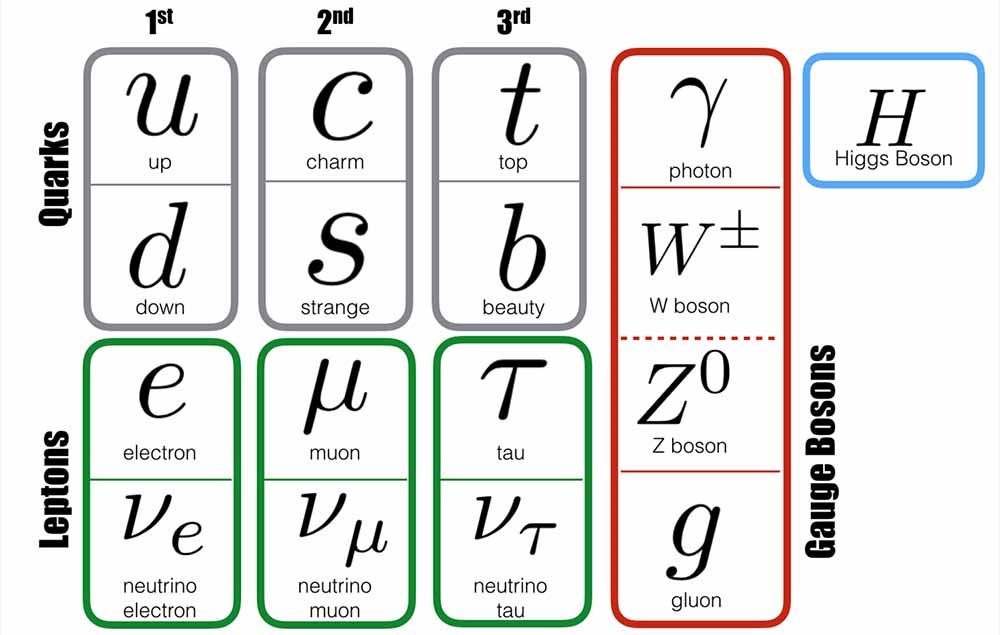
Podsumujmy, co wiemy. Mamy fermiony i bozony. Do fermionów należą kwarki górne, kwarki dolne, elektrony oraz okropnie trudne do schwytania neutrina elektronowe. Ale to dopiero początek. Jak stwierdziliśmy wcześniej, jedno z wielkich złamań symetrii doprowadziło do powstania fenomenu masy i wyodrębnienia zdeformowanych odbić każdej z tych drobin. W ten sposób obok elektronu funkcjonują masywniejsze mion oraz taon; obok neutrina elektronowego odpowiednio neutrino mionowe i taonowe; obok kwarka górnego kwark powabny i szczytowy; zaś obok kwarka dolnego kwark dziwny i spodni (patrz na powyższy schemat).
Dużo tego, prawda? Jednakże w tym bałaganie widać pewien porządek. Istnieją niejako trzy generacje cząstek: wersja normalna plus dwóch tłuściejszych krewnych. To nic innego jak odcisk utraconej symetrii, ślad pękniętego lustra. Gorzej mają się sprawy po wciągnięciu w to rozumowanie bozonów. Bo o ile znamy lub przynajmniej domyślamy się więzów pokrewieństwa między samymi cegiełkami materii, o tyle przejawów jakiegokolwiek powinowactwa między fermionami i bozonami – bytami o spinie połówkowym i tymi o spinie całkowitym – na pierwszy rzut oka w ogóle nie widać.
Oto superpartnerzy
Ten kłopot legł u podstaw prac nad kolejną, jeszcze bardziej złożoną i ogólniejszą symetrią, nazwaną pieszczotliwie SUSY – supersymetrią. To naturalna kolej rzeczy, jeśli chcemy marzyć o zaprojektowaniu faktycznej teorii wszystkiego. Co z tego, że potrafimy (przynajmniej na papierze) wymazać granice między kolejnymi cząstkami materii, skoro nadal pozostaną one niezwiązane z nośnikami oddziaływań. Jak szaleć to szaleć, jak unifikować to na całego.
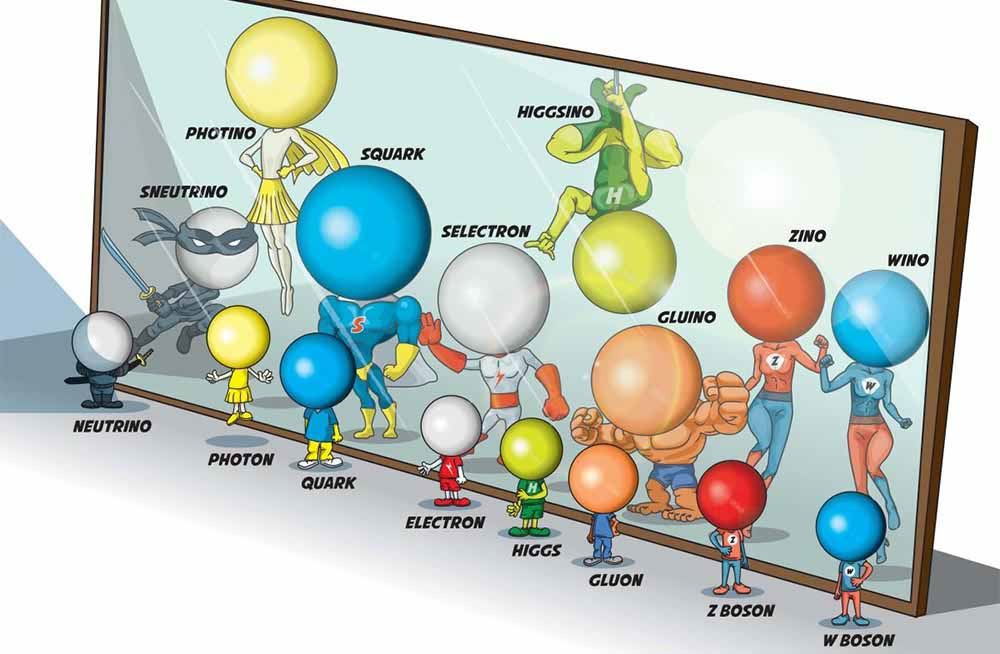
Poznajmy więc Susy – tajemniczą, ale i nieśmiałą damę. Chowa się przed światem, po cichu romansując z wszystkimi występującymi w naturze cząstkami, od gluonów po elektrony. Z prawdziwą gracją rozsiewa styl i elegancję w chaotycznym świecie kwantów. Co dla nas najważniejsze, posiada szczególną moc: każdy napotkany fermion przekształca w bozon, a każdy usidlony bozon w fermion. Innymi słowy zmienia spin każdego z zalotników o 1/2.
Potężna sypersymetria będzie dla nas kolejnym zwierciadłem, ujawniającym ukryte oblicza cząstek. Stojący przed nim kwark ujrzy swoje odbicie, dwojako zniekształcone: o spinie całkowitym oraz większej masie. Zobaczy skwark. W ten sposób, teoria zakłada istnienie całej menażerii nowych cząstek. Elektronom odpowiadają selektrony, neutrinom sneutrina, kwakrom wspomniane skwarki. Bozony również mają towarzystwo: fotina, gluina, zina, wina i grawitina. Zbiorczo noszą one miano superpartnerów. Tak jak ustaliliśmy, każdy superpartner bozonu jest fermionem, a superpartner fermionu bozonem.
Pewnie zapytasz dlaczego Susy dobiera się nie tylko do spinu obiektów, ale również zwiększa ich masę? Bo to założenie idealnie pasuje do naszych obserwacji, a właściwie ich braku. Skwarki, selektrony i sneutrina muszą być tak masywne, że energia dostępna w naszych akceleratorach nie pozwala na ich wytworzenie. Czy to nie nazbyt życzeniowe myślenie? Być może, stąd dzieje supersymetrii sięgające lat 70. są pasmem kolejnych kryzysów i spekulacji. To, jak bardzo świat nauki oczekuje dowodu na elegancję wszechświata, najlepiej obrazuje teza postawiona przez Marię Spiropulu z CERN-u:
Odkrycie supersymetrii byłoby wzniosłym wydarzeniem i myślę, że nawet większym niż odnalezienie życia na Marsie.
Maria Spiropulu
Na marginesie muszę dodać, że supersymetria jest wciąż ideą niezwykle żywą, którą gros fizyków próbuje dalej usprawniać i poprawiać. Jedną z ciekawszych wariacji, jednocześnie mocno ingerujących w rdzeń teorii, pozostaje symetria konforemna, której współautorem i orędownikiem jest profesor Uniwersytetu Warszawskiego, Krzysztof Meissner. Koncepcja ta rezygnuje z pomysłu dokooptowywania każdej znanej cząstce nieuchwytnego superpartnera. Zamiast tego, proponuje model zawierający tylko jedną nową cząstkę (czy też nową rodzinę cząstek): cięższego krewniaka bozonu Higgsa. Dlaczego akurat jego? Jeśli czytałeś ten tekst uważnie, być może dostrzegłeś, że wśród elementów modelu standardowego tylko higgson cechuje spin równy 0. Symetria konforemna zakłada istnienie jednej lub kilku cząstek o zerowym spinie. Jednak jak na razie brak eksperymentalnych poszlak wspierających ten czy inny zamysł.
Struny są super
Wiesz co jest w Susy najlepsze? Tak naprawdę nie stanowi ona konkurencji dla postulowanych kandydatek na teorię wszystkiego. Powinniśmy o niej myśleć raczej w kategoriach pewnego drogowskazu, czy może łatki możliwej do naklejenia na wiele współczesnych koncepcji fizycznych, czasem nawet niezwiązanych z planami wielkiej unifikacji. Weźmy choćby problem ciemnej materii, czyli enigmatycznej substancji stanowiącej większość masy wszechświata. Widzimy jej grawitacyjny wpływ na ciała niebieskie, ale nikt nie wie z czego może się składać. A przecież właśnie Susy oferuje nam całą gamę nieznanych i masywnych cząstek, których nikt dotąd nie widział. Kto wie, może fizycy upieką dwie pieczenie na jednym ogniu?
Najważniejszy pozostaje jednak wpływ supersymetrii na model standardowy oraz teorię strun, nazywaną po usprawnieniach niekiedy teorią superstrun. Już jej pierwotna wersja wyjaśniająca jedynie strukturę oddziaływań silnych zawierała spory zestaw symetrii, lecz tylko tych koniecznych do przenoszenia sił jądrowych. Przez ten fakt, zwykło się ją nazywać bozonową teorią strun. Dopiero po opublikowaniu publikacji Schwarza i Greena, struny zyskały nowy format. Teoretycy zdali sobie sprawę, że aby zunifikować grawitację z mechaniką kwantową, potrzebny będzie ogromny arsenał symetrii – największy jaki kiedykolwiek widziała fizyka.
Prace w tym kierunku prowadzili Ryan Rohm, Emil Martinec, Jeffrey Harvey i David Gross, znani w środowisku jako kwartet strunowy z Princeton. Dowiedli oni, iż właściwości struny pozwalają na zastosowanie wyjątkowej symetrii E(8)xE(8). Superstruny stały się tak potężne, iż nie tylko obejmowały dotychczasowy dorobek autorów teorii wielkiej unifikacji, ale również przynosiły wiele nowych rozwiązań. Jednocześnie, to właśnie rozległy repertuar symetrii wprowadził zamęt oraz najbardziej zwariowany postulat strunowców – większą liczbę wymiarów przestrzennych. Badacze nie do końca rozumieją przyczynę takiego stanu rzeczy, ale obliczenia dotyczące struny kwartetu z Princeton, ciągle wymagały takich liczb jak: 8, 10, 11 (choć akurat pomysł 11 wymiarów jest owocem późniejszych rozważań) i 26. Dopiero po takim rozszerzeniu przestrzeni, równania ujednolicające przyrodę stają się wolne od anomalii.
A jeśli teoria superstrun wyląduje w koszu? Nawet gdyby do tego doszło, sama idea supersymetrii prawdopodobnie będzie nadal funkcjonować i rzucać cień na wszystkie koncepcje zbliżające się do zjednoczenia praw natury. Symetrie wsiąkły w umysły fizyków tak głęboko, że ich respektowanie stało się niemalże metodologicznym nawykiem. Kiedy nie jesteśmy pewni, w którym kierunku podążyć, coraz częściej zdajemy się na trudne do zdefiniowania poczucie matematycznej i logicznej estetyki.
Ciąg dalszy nastąpi.











