Popularnonaukowe

Kosmiczna symfonia cz.3: Teoria strun

Odsłonięcie fundamentalnej zasady wszechświata, może wymagać od nas radykalnej zmiany paradygmatów i przyjęcia, że głównym budulcem rzeczywistości są maleńkie, wielowymiarowe kosmyki energii. Właśnie taką wizję proponuje nam teoria strun.

byAdam Adamczyk

12/01/2018

9 minute read

19 komentarzy

Czy to niesamowite? Wręcz niezwykłe? Ja to nazywam elegancją.
Walter Lewin

Szczęśliwy traf studenta

Doskonale pamiętam, że gdy po raz pierwszy pisałem o teorii strun jakieś osiem lat temu, to wszystkie artykuły na ten temat w polskojęzycznym internecie dało się zliczyć na palcach jednej ręki. Osoba postronna mogłaby wysnuć z tego faktu wniosek, że mowa o bardzo egzotycznej i nowatorskiej koncepcji, która jeszcze nie zdążyła trafić pod strzechy. Jednak rzeczywistość wygląda nieco inaczej. W istocie, struny można traktować w kategoriach naukowej egzotyki, ale ich dzieje sięgają równie głęboko co wielu innych, powszechnie znanych teorii fizycznych. Jednak podobnie jak choćby w przypadku słynnego bozonu Higgsa, potrzeba było całych dekad wzlotów i upadków, zanim strunowcy przepchali się do głównego nurtu nauki.

Wszystko zaczęło się w roku 1968, gdy Gabriele Veneziano – 26-letni doktorant pracujący w Europejskiej Organizacji Badań Jądrowych (CERN) – podobnie jak wielu starszych kolegów, głowił się nad istotą oddziaływania silnego. Było to świeżo po odkryciu wewnętrznej struktury hadronów i poznaniu zalegających w nich kwarków, ale jeszcze przed sformułowaniem zadowalającej teorii opisującej zachodzące między kwarkami zjawiska. Dopiero kilka lat później Murray Gell-Mann rozgryzł tę zagadkę, kładąc podwaliny pod chromodynamikę kwantową (QCD, co powinieneś pamiętać z poprzedniej części).

W każdym razie, zanim to nastąpiło, marzący o naukowych laurach Veneziano próbował samodzielnie zrozumieć, jak oddziaływanie silne zlepia kwarki wewnątrz protonów i neutronów. Podczas wielotygodniowego ślęczenia nad książkami wpadł mu w oko wzór, znany jako funkcja beta, przypisywana wielkiemu szwajcarskiemu matematykowi, Leonhardowi Eulerowi. Ku zdziwieniu młodego fizyka, relikt XVIII-wiecznej matematyki zdawał się świetnie odpowiadać na jego bolączki z oddziaływaniem silnym. Nie wiedział, dlaczego archaiczna formuła wydawała się niemal idealnie skrojona pod jego problem, ale oczywiście niezbyt to go w tamtej chwili interesowało.

Odpowiedź nieco później znaleźli, niezależnie od siebie, Yoichiro Nambu z Uniwersytetu w Chicago oraz Leonard Susskind z Uniwersytetu Stanforda (na zdjęciu poniżej). Oba nazwiska warto zapamiętać. Ten pierwszy, obdarzony nazbyt skromnym charakterem, nie pchał się na pierwsze strony gazet, przez co bywał często pomijany w popularnych opracowaniach. Przynajmniej do 2008 roku, gdy za swój wkład w analizę spontanicznego łamania symetrii, doczekał się nagrody Nobla. Natomiast Susskinda powinna kojarzyć każda osoba zainteresowana czarnymi dziurami, ponieważ to właśnie Amerykanin wygrał ważną batalię z samym Stephenem Hawkingiem, dotyczącą zasady zachowania informacji.

Współtwórca teorii strun – Leonard Susskind — Leonard Susskind – jeden z autorów i orędowników teorii strun.

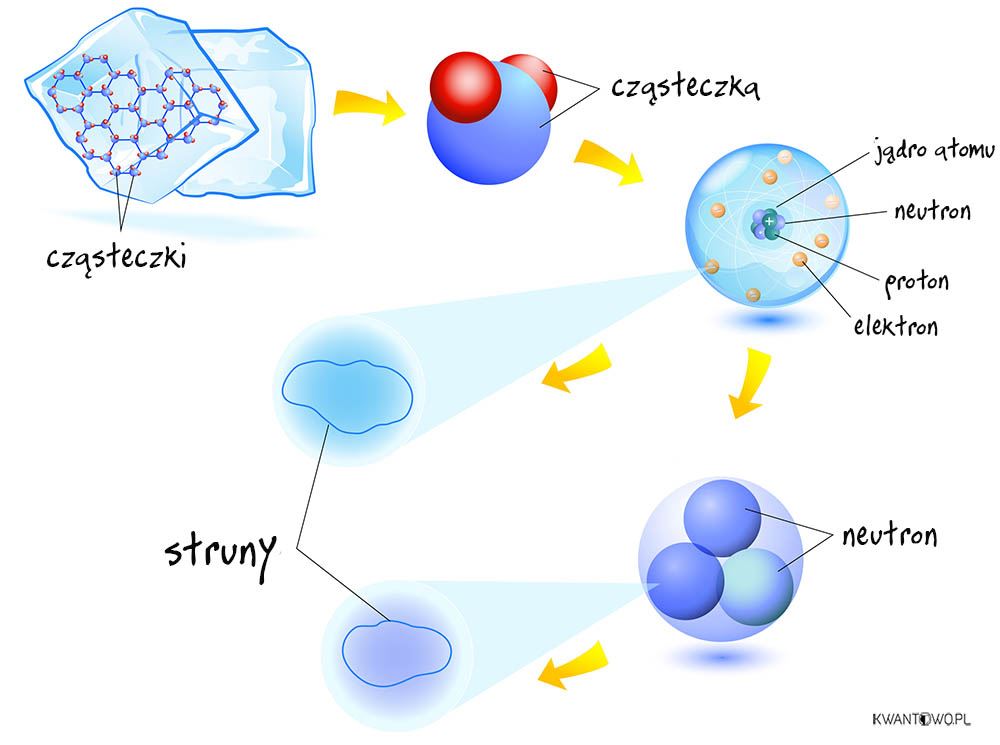
Obaj teoretycy, na podstawie dość szczęśliwego odkrycia Gabriele Veneziano, ukuli podstawowe równania dla nowej teorii. Wyróżniała ją jedna wyjątkowa cecha. Do tej pory, przedmiot zainteresowania fizyków mikroświata stanowiły byty punktowe. Nawet jeśli charakteryzował je dualizm korpuskularno-falowy, a zasada nieoznaczoności zabraniała jednoczesnego określenia ich pędu i lokalizacji – nadal myślano o cząstkach punktowych. Używając wysublimowanych słów, był to swego rodzaju paradygmat, pewien utrwalony sposób rozumowania. Nadchodząca rewolucja domagała się zmiany paradygmatu, wprowadzenia w miejsce klasycznych cząstek czegoś bardziej elastycznego. Zastąpienia ograniczonych punktów, krzywymi i pętlami.

Zamiana bazgrołów na rurki

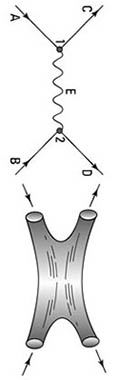
Spróbujmy zrozumieć, w jaki sposób nowe podejście do tematu wywracało dotychczasowe pojęcie o fizyce. Wyobraź sobie, że chcesz przedstawić na prostym wykresie historię dowolnej cząstki elementarnej. Oś pionowa wyznacza upływ czasu, a pozioma przestrzeń. Nie ma tu żadnego haczyka, “życie” przykładowej cząstki przybiera kształt linii, zależnie od przyjętej prędkości i upływu czasu. Mniej więcej na takiej zasadzie powstały diagramy Richarda Feynmana, które przedstawiały interakcje obiektów subatomowych, jako bazgroły pełne schodzących się kresek i strzałek. Przyjęcie idei Nambu i Susskinda, zmusiłoby nas jednak do zrewidowania tych prostych diagramów. Przedtem żywot cząstki w czasoprzestrzeni reprezentowała linia, bo samą cząstkę traktowaliśmy jako punkt, czyli byt zerowymiarowy (czy też bezwymiarowy). Jeżeli jednak cząstka to pętla – a więc twór przestrzenny, mający określoną długość – to jej istnienia w czasoprzestrzeni nie może już reprezentować jednowymiarowa linia. Strunowy wariant diagramów Feynmana, zamiast zwykłych kresek musi posługiwać się systemem rurek, bo właśnie kształt rurki zarysuje na wykresie pętla.

Chyba nawet intuicyjnie jesteś w stanie wyczuć, że taka reforma zmienia coś więcej niż tylko estetykę diagramu. Nasze czasoprzestrzenne rurki posiadają pewną powierzchnię. Ich połączenia wyglądają inaczej niż łączenia linii, jak również daje się zastosować bardziej złożone równania. To oznaczało więcej możliwości opisywania nowych zjawisk oraz dawało pole do unifikacji już starych. Na dodatek, struny sprawdzały się bardzo dobrze w kontekście oddziaływania silnego, jako obiekty do pewnego stopnia elastyczne i stawiające opór przy próbie rozciągnięcia. Trochę jak gumki recepturki. Rzecz jasna ówczesna wiedza o wnętrzach protonu i neutronu była nader skromna, więc żaden teoretyk nie mógł wiedzieć, dlaczego ta właściwość tak trafnie odpowiada obserwacjom. Dopiero wiele lat później badacze zdefiniowali efekt swobody asymptotycznej, obdarzający kwarki sporą dozą wolności, póki są blisko siebie, ale stawiającej twardy opór przy próbie ich oddalenia (więcej na ten temat przeczytasz w tekstach o kwarkach i gluonach, co teraz nie jest zbyt istotne).

Czy Veneziano, Nambu i Susskind zostali okrzyknięci duchowymi spadkobiercami Newtona, Einsteina i Heisenberga? Nie. Świat fizyki uznał nową teorię za abstrakcyjną ciekawostkę, niemającą nic wspólnego z rzeczywistością. Posiadała ona wciąż kilka matematycznych problemów, a przede wszystkim rychło zniknęło na nią zapotrzebowanie. Nim śmiała koncepcja okrzepła, została pogrzebana przez chromodynamikę kwantową i dobita jakiś czas później za sprawą modelu standardowego. Oddziaływanie silne spajające kwarki, doczekało się już rozwiązania na gruncie bezpieczniejszej teorii, niewymagającej od badaczy poświęcenia i przyjęcia wielu dziwacznych założeń.

Teoria strun wylądowała na cmentarzysku historii nauki.

Linie i pętle

Na szczęście nie wszyscy je przekreślili: kilku zapaleńców wciąż dostrzegało w oryginalnej idei ogromny potencjał. Przełom nastąpił w połowie lat 70. Wtedy to młody badacz John Schwarz, w przebłysku geniuszu zrozumiał, że struny wykorzystywano dotychczas w błędny sposób, nie dostrzegając ich rzeczywistego potencjału. Nie była to wcale koncepcja tłumacząca funkcjonowanie jądra atomowego, lecz potężna teoria obrazująca stosunki między wszelakimi cząstkami występującymi w przyrodzie! Nastąpił przełom. Wiele bolączek strun nagle okazało się ich zaletami, a całość mogła znaleźć od groma zastosowań. Schwarz podekscytowany wnioskami, szybko wciągnął do badań swojego kolegę, Michaela Greena. Obaj panowie kontynuowali pracę z dala od blasku reflektorów, dzięki czemu w spokoju eliminowali kolejne problemy. Wreszcie, po wielu latach żmudnych obliczeń, w roku 1984 Schwarz i Green opublikowali swoją wersję zapomnianej teorii strun, tym razem jako potencjalnej teorii wszystkiego. Artykuł spowodował naukowe trzęsienie ziemi. Entuzjaści strun w mgnieniu oka przestali być kilkuosobową grupką dziwaków, trafiając w samo centrum zainteresowania akademickiego. Setki młodych i ambitnych adeptów fizyki, a także wielu starszych, lecz wciąż wierzących w realizację marzenia Einsteina, prześcigało się w pomysłach na wykorzystanie strun w celu zunifikowania praw przyrody.

Schwarz i spółka zaproponowali całkowicie nowe spojrzenie na wszechświat. Teoria strun zakłada, że gdyby człowiek potrafił zajrzeć daleko w głąb cząstki elementarnej – obojętne czy rozważamy elektron, neutrino, kwark, gluon czy foton – ujrzałby maleńki, nieprzerwanie wibrujący kosmyk energii. Wszystko w swej istocie jest więc złożone z tego samego budulca: od DNA w naszym ciele, przez wodór w gwiazdach, aż po same nośniki oddziaływań i pola kwantowe. Skąd więc cała kosmiczna różnorodność? Klucz stanowi podstawowa właściwość strun – ich drgania – wieczne konwulsje wymuszane przez Wernera Heisenberga i jego zasadę nieoznaczoności. Tę samą, która wywołuje nieustanne fluktuacje kwantowe i zabrania subatomowym tworom posiadania jednocześnie określonego pędu i położenia. Struna w cząstce, niczym struna gitary, zależnie od szarpnięcia zmienia ton, przyjmując tym samym określone właściwości.

Pięknej metafory użył Michio Kaku, mówiąc, iż rodzaje cząstek “nie są niczym innym, jak różnymi nutami wygrywanymi na superstrunie. Harmonia tej struny to prawa fizyki”. Już w latach 80. wyliczono właściwości strun dla poszczególnych cząstek, w oparciu o prostą zasadę (i mniej proste wyliczenia). Z im bardziej napiętą struną mamy do czynienia, tym trudniej nam ją dostrzec i wyczuć jej obecność. Idąc tym tokiem rozumowania, byle elektron skrywa w swoim sercu dość luźną strunę, podczas gdy hipotetyczny grawiton dysponuje struną naprężoną do granic możliwości. Kwant pola grawitacyjnego do chwili obecnej umyka eksperymentatorom, ale jak powszechnie wiadomo, sama grawitacja jest bezsprzecznie najsłabszym z czterech oddziaływań podstawowych. W każdym momencie gdy wstajesz rano z łóżka, mięśnie Twojego ciała pokonują siłę grawitacji całej planety. Według teorii strun, duże napięcie struny oznacza niejako uwięzienie weń energii i znaczne osłabienie jej wpływu na otoczenie. Patrząc od drugiej strony, naprężenie grawitonów mogłoby również tłumaczyć dlaczego sieć czasoprzestrzenna wydaje się tak sztywna i dlaczego potrzeba ciał o ogromnych gabarytach aby wywrzeć mierzalny efekt grawitacyjny.

Mała metodologiczna dygresja

Czy teoria może być hipotezą? Czy hipoteza może być nazwana teorią? To pytania, które na pewno zaświtały przynajmniej części z czytelników, zwłaszcza jeśli (podobnie do mnie) przywiązują wagę do metodologicznej precyzji. W niemal każdym opracowaniu, jak również w tym cyklu artykułów, nieustannie pojawia się nazwa teorii strun. Jednak z punktu widzenia czystej metodologii fizyki taki tytuł wydaje się co najmniej dyskusyjny. Teoria to taki opis zagadnienia, który już przeszedł pomyślnie jakąś formę weryfikacji i stanowi jego najlepsze wyjaśnienie, zgodnie z aktualnym stanem wiedzy. Jakby na to nie spojrzeć, struny to dla fizyki hipoteza – przypuszczenie, niestety wciąż dalekie od przetestowania. Na próżno również szukać tu spełnienia popperowskiego kryterium falsyfikowalności.

Dlaczego więc do strun przylgnęło doniosłe miano teorii? Najczęściej wskazuje się na matematyczną wartość pracy Nambu, Susskinda i ich następców. Pod tym względem, jako pewien szczególny formalizm, teoria strun kwalifikuje się do tytułu teorii matematycznej. Osobiście rozważam też, czy takie nazewnictwo nie jest pewnym zabiegiem marketingowym. Wszakże każdy naukowiec chciałby aby jego dziecko zyskało jak największy prestiż, przynosząc twórcy wieczny splendor. Jednak zachowując rygor, jak najbardziej można myśleć o strunach w kategoriach fizycznej hipotezy i sądzę, że sami jej autorzy raczej nie rozdzieraliby szat.

A Ty w ilu wymiarach żyjesz?

Od samego początku nie brakowało zawziętych krytyków strun, i nie zaprzeczę, że byli uzbrojeni w arsenał trafnych argumentów. Dwa problemy wydają się szczególnie dotkliwe i prawdopodobne, że nigdy nie doczekają się rozwiązania.

Pierwszy jest związany z jeszcze jedną wyjątkową właściwością strun, o której wcześniej nie wspomniałem, a o której być może słyszałeś. Mianowicie, struny już w czasach Nambu i Susskinda sprawowały się najlepiej gdy posiadały znacznie więcej swobody niż dawała im nasza czterowymiarowa czasoprzestrzeń. Nie owijając w bawełnę, koncepcja pozbywała się wszelkich matematycznych anomalii dopiero gdy rozważało się jej funkcjonowanie w… 26 wymiarach!

Wiedz, że sam zamysł dodatkowych wymiarów wcale nie należał do fizycznych nowinek. Już wiele dekad wcześniej Theodor Kaluza proponował Einsteinowi dokooptowanie kolejnego wymiaru przestrzennego w celu połączenia grawitacji z elektromagnetyzmem. Różnica sprowadzała się do tego, że wtedy dodatkowy wymiar miał być “większy” i obejmować pozostałe cztery, zaś według strunowców, 22 wymiary powinny pozostawać zwinięte do rozmiarów mikroskopowych. Poza tym, Kaluza mówił o pięciu wymiarach, a nie o totalnie zwariowanej liczbie 25 wymiarów przestrzennych i jednym czasowym… To mogło ostudzić zapał, nie tylko wśród konserwatywnych uczonych. Podobno sam Richard Feynman traktował struny z przymrużeniem oka, a kolegów zajmujących się tym tematem lubił irytować pytaniami typu: “a w ilu wymiarach dzisiaj żyjemy”? Ostatecznie noblista nie wykluczał poprawności równań Schwarza i Greena, ale stał na stanowisku, że równie dobre rezultaty może w przyszłości przynieść inna, mniej ekstrawagancka teoria.

Drugi defekt teorii strun dotyczy jej weryfikowalności. Fizyka, jako nauka ściśle empiryczna, domaga się doświadczeń i obserwacji. Przeprowadzenie eksperymentu pozwalającego na bezpośrednie uchwycenie struny możemy w zasadzie uznać za niemożliwe z bardzo prozaicznego powodu. Mówimy o bardzo małych strukturach. Bardzo, bardzo, bardzo, bardzo, bardzo małych; ocierających się o najmniejszą wielkość mającą sens fizyczny, czyli długość Plancka, wynoszącą 10^-35 metra, lub jeśli wolisz, kwintyliardową część milimetra.

Gdybyśmy zbudowali model atomu rozmiarów Ziemi, to w tej skali pojedynczy proton osiągnąłby wielkość zbliżoną do Piramidy Cheopsa, a struna wciąż pozostawałaby znacznie mniejsza od jądra atomu! Nie zbudujemy wystarczająco czułego mikroskopu, bo wielkość elektronu, nie mówiąc o długości fali świetlnej, nigdy nie pozwoli na zarejestrowanie tak drobnego obiektu. (Na marginesie, z tej samej przyczyny cudne ilustracje przedstawiające iskrzące kolorami struny, należy traktować wyłącznie jako barwne popisy grafików. Z racji swoich gabarytów struna sama w sobie nie może świecić ani posiadać koloru. Wspominam tak, na wszelki wypadek).

Co bardziej nietypowe, słabym punktem teorii strun okazało się również jej bogactwo – co wbrew pozorom, nie jest zbyt pożądanym stanem rzeczy w fizyce. W kolejnych latach naukowcy zauważyli, że ich koncepcja stała się tak piękna i elastyczna, iż daje się ją stosować aż na pięć różnych sposobów. Innymi słowy, odnaleziono pięć równie poprawnych wariacji teorii prowadzącej do zunifikowania praw przyrody. Ostatecznie poradzono sobie z tą klęską urodzaju, poprzez sformułowanie wzbudzającej ciarki M-Teorii. Ale to materiał na osobną odsłonę tego cyklu.

Jak wyłuskać prawdę?

Pisząc powyższy tekst uświadomiłem sobie, że struny będą niebawem obchodzić okrągłą, pięćdziesiątą rocznicę urodzin. Już pół wieku minęło od ukucia przez młodego Gabriele Veneziano – obecnie sędziwego profesora Collège de France – pierwotnych równań teorii, mającej początkowo opisywać silne oddziaływanie jądrowe. Mimo upływu całej epoki i wielu usprawnień, teoretyków wciąż nękają te same utrapienia. Pojawia się pytanie, czy brak szans na bezpośrednią detekcję powinien przekreślić hipotezę? A może w bliżej nieokreślonej przyszłości znajdziemy dostatecznie zadowalające dowody pośrednie?

Moim zdaniem największe osiągnięcie strunowców stanowi sama próba obalenia paradygmatu punktowych cząstek, jako podstawowego składnika wszechświata. Z wielu powodów, już przed wiekami w umyśle człowieka zarysował się obraz atomu o kształcie kulistym, składającego się z punktów bądź mniejszych kulek. Teoretycy strun zwrócili uwagę na banalny fakt: to co z daleka wydaje się punktem, w przybliżeniu wcale nim być nie musi. Ta idea ma szansę przetrwać, nawet jeżeli cała reszta teorii znów wyląduje w koszu. Co by nie mówić, wprowadzenie krzywych i pulsujących pętli, nadaje fizyce trudną do zdefiniowania elegancję. Jest coś pociągającego w myśli, że na fundamentalnym poziomie rzeczywistości wszystko toczy się w rytm kosmicznej symfonii. Symfonii strun.

Ciąg dalszy nastąpi.