Nobel za topologiczne stany materii – krótko i niezbyt przejrzyście

Wczorajsza nagroda Nobla spędza sen z powiek dziennikarzom, komentatorom i popularyzatorom. Nie tylko dlatego, że topologiczne przejścia fazowe zostały wyróżnione dość niespodziewanie, ale również ze względu na ogromną zawiłość tego tematu.

Nie będę wyjątkiem. Nazwiska Davida Thoulessa, Duncana Haldane’a i Michaela Kosterlitza, jak i ich prace, pozostawały dla mnie anonimowe. Przeszukując całą podręczną literaturę trafiłem tylko na tego pierwszego, wspomnianego mimochodem jako laureata nagrody Wolfa. Tak jak większość osób spodziewałem się raczej wyróżnienia odkrywców fal grawitacyjnych, pracujących przy detektorze LIGO. Tu, jak sądzę, na przeszkodzie mógł stanąć kłopot z wypchnięciem przed szereg konkretnych kilku ludzi, spośród kilkutysięcznej rzeszy uczonych. Oczywiście mniejsza medialność danych dociekań nie powinna decydować o ich rzeczywistej wartości. A plus jest taki, że tegoroczny Nobel zamknie usta malkontentom psioczącym na ciągłe honorowanie teoretyków oraz ich “niepraktycznych odkryć”. Akurat tym razem doceniono badania o bezpośrednim znaczeniu dla techniki i technologii.

Niestety, nie jestem w stanie przybliżyć Wam detali tak wyrafinowanych i specjalistycznych prac. Nawet prof. Meissner wspomniał dziś, że to bodaj najtrudniejszy do przystępnego wyłożenia temat, jaki przedarł się na szerokie medialne wody, w ostatnich dekadach. Jednak aby nie czuć wyrzutów z powodu niespełnionego obowiązku, spróbuję przynajmniej zarysować istotę zainteresowań trójki brytyjskich fizyków.

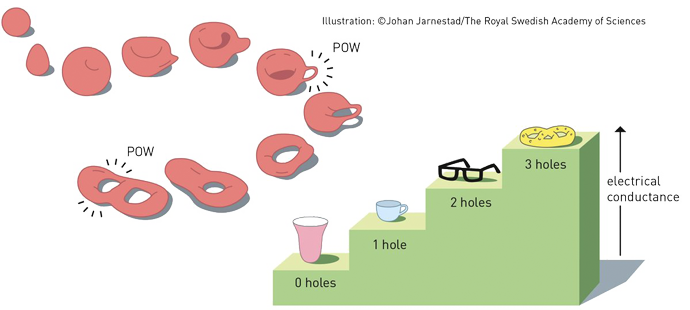
Na początek spróbujmy uprościć terminologię. Topologia to dziedzina matematyki dotycząca przekształceń przestrzeni czy obiektów geometrycznych – stąd czasami mówi się o “elastycznej geometrii”. Szczególną atencją topologów obdarzane są takie własności figur, które nie znikają mimo ich odkształcania. Najlepiej zobrazował to członek komisji noblowskiej, korzystający z przyniesionego zestawu rekwizytów, pod postacią… precli i obwarzanków. Z punktu widzenia topologii obwarzankowi bardzo blisko do opony, kubka czy igły. Każdy z tych przedmiotów posiada dokładnie jeden otwór i można sobie wyobrazić subtelne przekształcenie jednego w drugi, bez żadnych cięć i przerwania ich powierzchni. Precel z dwoma lub trzema dziurami, choć z ludzkiego punktu widzenia wydaje się bliźniaczym wypiekiem, topologicznie jest już tworem obcym. Takiemu preclowi, matematycznie bliżej chociażby do okularów.

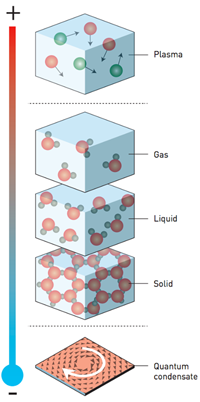
Drugie ważne pojęcie to przejście fazowe. Termin dość szeroki, ale w naszym kontekście można go porównać do zmian w stanie skupienia materii. Jak doskonale każdy z nas wie, ogrzewając lub oziębiając poszczególne substancje, możemy doprowadzić do ich zamarznięcia, roztopienia lub wyparowania. Na poziomie mikroskopowym oznacza to przede wszystkim zmiany w ruchu i uporządkowaniu atomów lub cząsteczek, a co za tym idzie, zmiany właściwości fizycznych. Z innym typem przejścia fazowego mamy do czynienia gdy w miarę obniżania temperatury w materiale zanika opór elektryczny, czyli ujawnia się efekt nadprzewodnictwa. Kosmologowie z kolei, zastanawiają się nad tym czy do przejścia fazowego nie doszło w pierwszym ułamku sekundy po wielkim wybuchu, co doprowadziło do inflacji przestrzeni. Mówiąc krótko, zmianą fazową nazwiemy nagłe przemiany własności fizycznych obiektów.

Teraz połączmy to w całość. Thouless, Haldane i Kosterlitz poszukują odpowiedzi na to, jak zmiany w topologii badanego ciała, wpływają na jego właściwości fizyczne. Nie chodzi tu jednak o byle jakie ciała. Ich głównym przedmiotem zainteresowań pozostają wyjątkowe struktury: najcieńsze jakie tylko można sobie wyobrazić, bo o grubości jednego atomu. Niektórzy – chyba słusznie, zważywszy na pojawiające się możliwości – traktują dwuwymiarowe materiały jako nowy, unikatowy stan materii. Tego typu nanosieci znamy już od dawna, czego przykładami są fosforen, stanenen, borofen, czy wreszcie bardzo medialny grafen. Wkładem badawczym noblistów jest analiza topologiczna tychże struktur. Przekładając to na naszą rzeczywistość: to trochę tak jak gdybyśmy dziurawili na różne sposoby kawałek blaszki, a następnie testowali jak wpłynęło to na jej właściwości – zwłaszcza na jej przewodnictwo elektryczne.

Po co to? Okazuje się, że takie drobne zmiany w topologii mogą doprowadzić nas do otworzenia nowych ścieżek w materiałoznawstwie. Łatwo wyobrazić sobie superkomputery wykorzystujące nanostruktury o niemal zerowym oporze elektrycznym. Obecnie nie jest to takie proste, ponieważ “zwykłe” substancje wymagają utrzymywania niedorzecznie niskiej temperatury dla ujawnienia swojego potencjału.

Na zakończenie kilka słów od Stevena Bramwella z London Centre for Nanotechnology:

Myślę, że ta nagroda Nobla jest niezwykle zasłużona! Zachowanie materiałów wokół nas jest bardzo skomplikowane – zadaniem fizyki pozostaje określenie prostych zasad, dzięki którym będziemy mogli zrozumieć świat materiałów i przewidywać nowe zjawiska. Jest to bardzo trudne wyzwanie, ponieważ przeciętna substancja może zawierać biliony bilionów atomów, wchodzących ze sobą w interakcję na różne sposoby.

Pomysłowość Kosterlitza, Thoulessa i Haldane’a polegała na ukazaniu, jak duża jest klasa materiałów – zwłaszcza sieci i łańcuchów atomów – które można rozumieć dzięki prostym zasadom topologii. Przełom zapoczątkowany przez tych trzech naukowców pozwoli na ogromne postępy w zrozumieniu i opisie właściwości wielu systemów materiałowych. W moim przypadku, od 25 lat otwarty jest temat magnetycznych właściwości cienkich struktur – czyli tego co można zastosować choćby w dyskach komputerów do przechowywania informacji. Wielu innych naukowców, w wielu dyscyplinach będzie miało dług wdzięczności do teoretycznych spostrzeżeń Kosterlitza, Thoulessa i Haldane’a.