Nobel za test najważniejszej nierówności świata – rozwlekle, ale za to niezbyt przejrzyście

Po laurach dla fizyków atmosfery, astronomów i kosmologów w poprzednich latach, komisja w Sztokholmie wreszcie uśmiechnęła się do fizyków kwantowych. Noblem za rok 2022 podzielili się Alain Aspect, John Clauser oraz Anton Zeilinger. Jak głosi oficjalne uzasadnienie, Francuz, Amerykanin i Austriak zostali docenieni za eksperymenty nad układami splątanych fotonów, które pozwoliły na potwierdzenie, że w mikroświecie nierówności Bella nie są zachowane. Chyba nie przesadzę, stwierdzając, że to jedno z najbardziej spodziewanych wyróżnień ostatnich dekad. Zaskakiwać może jedynie fakt, że badania, które przyniosły jeden z najważniejszych wniosków XX-wiecznej fizyki, musiały czekać na docenienie tak długo.

Jeżeli zakończyliście swoją przygodę z mechaniką kwantową na zamykaniu pudła z kotem Schrödingera, macie prawo czuć się nieco zagubieni. O ile o splątaniu każdy coś tam słyszał, to kim jest ten cały Bell? Dlaczego powinna interesować nas jego nierówność i jej testowanie?

Żeby to pojąć, musicie wiedzieć, że konstrukcja wznoszona przez pokolenie Bohra, Heisenberga, Schrödingera, Einsteina, czy Diraca, bynajmniej nie została ukończona. Postawili oni grube ściany, sufit, nawet dołożyli parę dachówek, ale równocześnie dali ciała już na etapie wylewania fundamentów. Mianowicie, mimo dekad sporów, dawni mistrzowie nie zdołali wypracować porozumienia na temat problemu ukrytych zmiennych. Kiedy jedni fizycy uważali, że cząstki przybierają określony stan dopiero w momencie pomiaru, inni zakładali, że wszystkie parametry stale i obiektywnie istnieją, choć cząstka nie zawsze chce nam je zdradzać.

Problem z całą mocą ujawniał się w kontekście efektu splątania kwantowego. Skrzętnie wykorzystali to Einstein, Podolsky i Rosen, wykuwając w 1935 roku eksperyment myślowy, znany dziś pod nazwą paradoksu EPR. Wiedzieli oni, że cząstki lub atomy da się skorelować ze sobą w taki sposób, aby nawet po odseparowaniu nadal dzieliły określone właściwości. Oznacza to, że łapiąc jeden z obiektów i poznając jego cechę (np. spin lub polaryzację), automatycznie poznajemy też cechę tego drugiego.

Zdaniem tercetu EPR istniały dwie możliwości tłumaczące ten fenomen. Pierwsza była taka, że zgodnie z kwantowymi prawidłami, cząstki pozostają w nieokreślonym stanie do momentu obserwacji, przy czym pomiar jednej z nich konkretyzuje automatycznie stan drugiej. Działoby się to natychmiast, bez względu na dystans, co Einstein ochrzcił mianem “upiornego działania na odległość”. Według drugiej opcji, splątane cząstki nie różniłyby się od rozdzielonej pary rękawiczek, umieszczonych w zamkniętych pudełkach. Jeżeli w jednym z pudeł znajdziemy rękawiczkę lewą, od razu będziemy wiedzieć, że w drugim cały czas leżała prawa. Właściwości obu paczek byłyby zdefiniowane od samego początku, choć na pierwszy rzut oka pozostawałyby niewidoczne – analogicznie do zmiennych ukrytych.

Dylemat niemalże filozoficzny, ale pewien naukowiec znalazł w końcu sposób na jego rozstrzygnięcie z matematyczną precyzją. Był nim wielki nieobecny ostatniej ceremonii noblowskiej, czyli John Stewart Bell^[1]Zmarł przedwcześnie w wieku 62 lat wskutek krwotoku mózgowego. Gdyby żył, bez wątpienia również zostałby nagrodzony Noblem.. Urodzony w Belfaście teoretyk sformułował twierdzenie mające służyć odróżnieniu par posiadających trwale zapisane cechy od takich, które konkretyzują swój stan dopiero w chwili badania. Odseparowaniu korelacji klasycznych od korelacji rządzonych kwantowymi regułami gry.

Dobra wiadomość jest taka, że powstały dziesiątki sposobów ilustrowania nierówności Bella, dostosowanych do odbiorców o dowolnym stopniu zaawansowania. Zła natomiast, że nawet najprostsze z nich zajmują sporo miejsca i wymagają odrobiny cierpliwości przy analizowaniu danych. Myślę, że nie będę wymyślał koła na nowo i sam posłużę się klasycznym przykładem, opracowanym podobno przez Eugene’a Wignera (faceta, który kreatywnie rozwinął eksperyment myślowy z kotem Schrödingera), a chętnie wykorzystywanym również m.in. przez jednego ze świeżo upieczonych noblistów, Antona Zeilingera.

Bliźniaki Bella

W przykładzie tym, odpowiedniki cząstek stanowią ludzie, a konkretniej pary bliźniąt o trzech wyróżnionych zestawach cech wyglądu. Powiedzmy, że każdą jednostkę ocenimy przez pryzmat koloru włosów (brunet albo blondyn), barwy oczu (niebieskie albo zielone) oraz wielkości nosa (duży albo mały). Trzy cechy, a każda może przyjąć tylko jedną z dwóch wartości. Jeżeli zaprosimy do eksperymentu dużą liczbę takich par bliźniąt, zauważymy, że istnieje osiem możliwych kombinacji wyglądu dla każdej osoby: niebieskooki brunet z dużym nosem, zielonooki brunet z dużym nosem, niebieskooki brunet z małym nosem… No dobra, może to rozrysujmy.

Bez względu na to, czy będziemy mieli do czynienia z setkami, tysiącami, czy miliardami par bliźniąt, logika zawsze będzie pozwalała nam na wysunięcie pewnych wniosków.

Przykładowo, łączna liczba bliźniąt niebieskookich z wielkimi nosami powinna być równa liczbie bliźniaków z niebieskimi oczami, wielkimi nosami i blond włosami zsumowanej z liczbą bliźniaków z niebieskimi oczami, wielkimi nosami i włosami brązowymi. Trudno, żeby było inaczej, skoro pierwszy zbiór zawiera w sobie dwa kolejne. Podobnie, mamy prawo zakładać, że dajmy na to, liczba niebieskookich bliźniąt z wielkimi nosami, w każdym przypadku będzie mniejsza lub równa od liczby bliźniąt obdarzonych wielkimi nosami i brązowymi włosami zsumowanej z liczbą bliźniąt o niebieskich oczach, wielkich nosach i blond włosach.

Bawiąc się z trzema dostępnymi parametrami, można wymyślić wiele tego rodzaju prostych równości lub nierówności. Jednak John Bell rozważał bardziej pogmatwaną sytuację, w której badając pary bliźniąt, możemy zapytać o tylko jedną cechę danej osoby. Taka relacja może wyglądać np. w taki sposób.

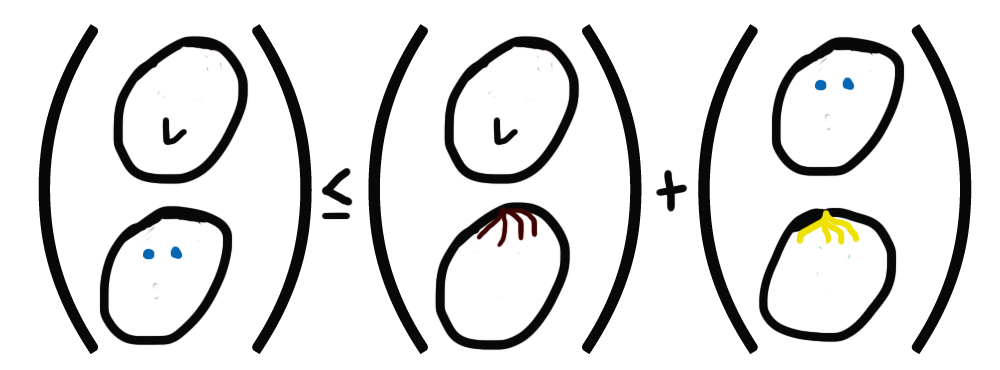
Sformułowana w ten sposób nierówność musi zostać spełniona, jeżeli tylko przyjmiemy zdroworozsądkowe założenie, że bliźniacy pozostają podobni i nie odwiedzą fryzjera, ani nie przejdą operacji plastycznej. Nie musimy widzieć wszystkich cech, bo wiemy, że niebieskie oczy u jednego brata oznaczają również niebieskie u drugiego i tak dalej. Takie rozumowanie sprawdzi się w przypadku wszelkich par obiektów dzielących te same cechy. Przynajmniej w rzeczywistości dużych obiektów.

John Bell postawił sprawę jasno. Jeżeli sformułowana przez niego nierówność pozostaje zachowana w mikroświecie, będzie to znaczyło, że cząstki elementarne definiują pewne ukryte parametry, a Einstein miał rację przypisując przyrodzie deterministyczny charakter. Scenariusz taki bywa również nazywany lokalnym realizmem. Jeśli zaś nierówność podlega łamaniu, fizycy będą musieli pogodzić się z myślą, że kwantowa nieintuicyjność, z całym bagażem jej dziwactw, to po prostu immanentna cecha rzeczywistości.

W teorii, gdzie do mechaniki kwantowej dodano pewne parametry pozwalające określić wyniki pojedynczych pomiarów, tak by nie zmienić jednocześnie przewidywań statystycznych, musi istnieć też mechanizm, który powoduje, że zmiana ustawienia jednego z instrumentów pomiarowych może wpłynąć na odczyty innego instrumentu, niezależnie od odległości. Co więcej, związany sygnał musiałby być przekazywany natychmiastowo.

John Bell, 1964

Bell rozpisał nawet projekt eksperymentu, polegającego na pomiarach spinu splątanych atomów, wyrywanych z molekuł cząsteczkowego wodoru. Teoretyk nie wcielił jednak swojego pomysłu w życie, pozostawiając to wyzwanie bardziej zaawansowanym technicznie kolegom po fachu.

I tu pojawiają się nazwiska tegorocznych noblistów. Pierwszą próbę przeprowadzenia testu podjął w 1972 roku zespół Johna Clausera z Berkeley. Już tamte wyniki świadczyły o pogwałceniu nierówności Bella, ale uzyskane dane uznano za niewystarczające. Niekwestionowanego rozstrzygnięcia dostarczył dekadę później Alain Aspect, wraz ze swoimi współpracownikami z Instytutu Optyki Teoretycznej Orsay w Paryżu. Z kolei ekipa Antona Zeilingera z Uniwersytetu Wiedeńskiego (znana też z innych kwantowych wyczynów), dokończyła sprawę, dokonując prób w kolejnych wymyślnych wersjach i konfiguracjach^[2]Szczególne wrażenie robi “kosmiczny” test twierdzenia Bella, przeprowadzony w 2017 roku i dotyczący światła gwiazd..

Opis choćby jednego z tych doświadczeń, stanowiłby materiał wystarczający do wypełnienia rozdziału ceglastej księgi. Spróbujmy jednak uchwycić sedno sprawy, wspólne dla wszystkich przywołanych badań.

Każdy z zespołów operował na parach splątanych fotonów, wypuszczanych ze wspólnego źródła w przeciwległych wiązkach i przepuszczanych przez dwa urządzenia pomiarowe. Najprostszym wyborem są w tej sytuacji obrotowe płytki polaryzacyjne, które sprawiają, że foton – zależnie od tego, czy jest względem niej spolaryzowany pionowo, czy poziomo – może przejść dalej albo zostać zatrzymany. Wystarczy umówić się, że urządzenia będą miały trzy ustawienia (np. 0°, 120° i 240°), a uzyskamy sytuację analogiczną do naszych metaforycznych “bliźniaków”. Tyle tylko, że zamiast włosów, nosów i oczu, interesować nas będzie polaryzacja względem trzech różnych kierunków. Brzmi skomplikowanie, ale jeżeli spróbujemy sobie to zwizualizować, doliczymy się ośmiu dostępnych kombinacji.

Poza konfiguracją pierwszą i ostatnią, w każdym innym przypadku, mierząc stan cząstki na dowolnym z ustawień, otrzymujemy nie mniej niż 33% i nie więcej niż 67% szans uzyskanie przeciwnego wyniku w drugim detektorze. Moglibyśmy prowadzić eksperyment jak długo chcemy, bez przerwy losowo obracając płytkami i statystycznie nie powinniśmy wypaść poza te widełki. Pamiętajmy jednak, że wszystko, o czym teraz mówimy opiera się na założeniu, że fotony noszą w sobie ukryte parametry, zdefiniowane od momentu splątania. Tak, jakby umówiły się wcześniej, co do odpowiedzi, jakich udzielą na trzy możliwe pytania.

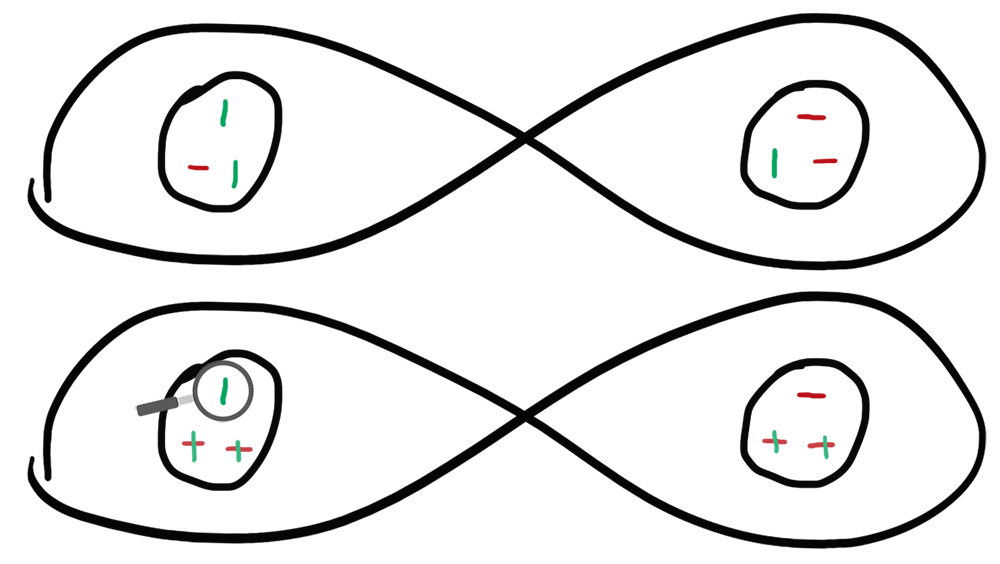
Przewidywania mechaniki kwantowej wyglądają nieco inaczej. Przede wszystkim, ustawiając aparaturę w dany sposób, powiedzmy na 120°, zmuszamy cząstkę do określenia swojego stanu jedynie dla tej sytuacji, nadal nie znając jej polaryzacji przy kącie 0° i 240°. Oznacza to, że o ile w obu urządzeniach będziemy badali to samo, otrzymamy spodziewany, przeciwstawny wynik; ale kiedy zaczniemy bawić się polaryzatorami na chybił trafił, w końcu spadniemy poniżej margines wynikający z tez Bella.

Docieramy do momentu, gdzie zdrowy rozsądek diabli biorą. W zamian dostajemy nowe, kwantowe minimum na poziomie 25%^[3]Jeśli musicie wiedzieć: interesuje nas cosinus kąta między pozycjami detektora (φ) podniesiony do kwadratu. Przy rozstrzale 120° daje to wynik 0,25. Według kwantowych prawideł nie powinniśmy spadać poniżej tej granicy. oraz nieco odświeżony rozkład prawdopodobieństw dla poszczególnych kątów.

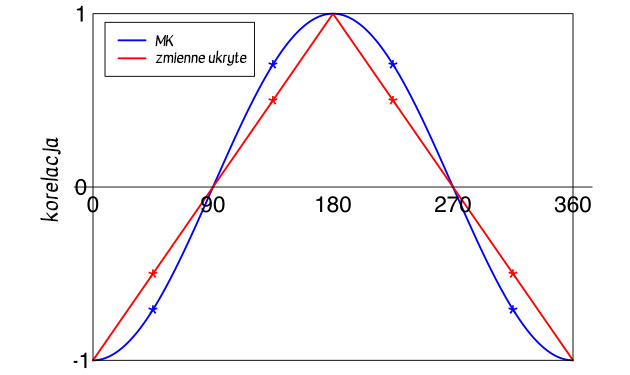
Wynik już znacie. Każdy z przeprowadzonych eksperymentów, dobitnie wskazał na drugi – ten kwantowy – koszyk danych i naruszenie nierówności Bella. To naprawdę oszałamiający wniosek o dalekosiężnych skutkach. Wiemy, że cząstka w momencie splątywania nie zabiera z sobą żadnej twardej instrukcji postępowania i wybiera odpowiedź dopiero w chwili przejścia przez polaryzator. Wiemy też, że jej partner, na przekór paradoksowi EPR, natychmiast “wie”^[4]U Aspecta oba detektory dzieliło 13 metrów, a dane były zbierane z dokładnością do 0,0000005 sekundy. Foton musiałby “informować” partnera o swoim wyborze szybciej od światła., że w analogicznej sytuacji powinien udzielić odpowiedzi przeciwnej – jak gdyby układ wiązała głęboka więź ignorująca przestrzeń.

Nasze wyniki, zgadzające się doskonale z przewidywaniami mechaniki kwantowej, stanowią z wysoką statystyczną pewnością silne dowody przeciwko szerokiej klasie teorii opartych na koncepcji lokalnego realizmu. Co więcej, nie zaobserwowano też żadnego wpływu odległości między punktami wykonywania pomiarów na rejestrowane korelacje.

Alain Aspect, 1981

Nie ulega wątpliwości, że próba Aspecta (i jej wariacje), należą do najdonioślejszych doświadczeń naukowych ubiegłego stulecia, a wielu fizyków określiłoby je najważniejszym testem dla mechaniki kwantowej (no, może za doświadczeniem z dwiema szczelinami). Uczeni za jednym zamachem, rozprawili się z rzekomymi ukrytymi zmiennymi, wyjaśnili paradoks EPR i mocno nadwyrężyli całą ideę lokalnego realizmu. I tak, zgodnie z zapowiedzią samego Johna Bella, obalenie jego fundamentalnej nierówności, stało się koronnym argumentem w sporze o naturę kwantowej rzeczywistości.

Chyba już pora na dzwonek^[5]Długo wstrzymywałem się z tym sucharem. :).

Literatura uzupełniająca:
J. Bell, On the Einstein, Podolsky, Rosen paradox, “Physics”, 1964;
A. Aspect, J. Dalibard, G. Roger, Experimental test of Bell’s inequalities using time-varying analyzers, “Physical Review Letters”, vol. 49, 1982;
E. Wigner, On Hidden Variables and Quantum Mechanical Probabilities, “American Journal of Physics” t. 38, 1970;
I. Czerwonogóra, Eksperyment myślowy EPR a spór o przedmiot mechaniki kwantowej, “Nowa krytyka”, t. 6, 1995;
A. Zeilinger, Od splątania cząstek do kwantowej teleportacji, przeł. B. Bieniok, E. Łokas, Warszawa 2013;
J. Baggot, Teoria kwantowa. Odkrycia, które zmieniły świat, przeł. J. Skalska, Warszawa 2013;
D. Schneider, Bell’s Theorem with Easy Math, [online: http://www.drchinese.com/David/Bell_Theorem_Easy_Math.htm].