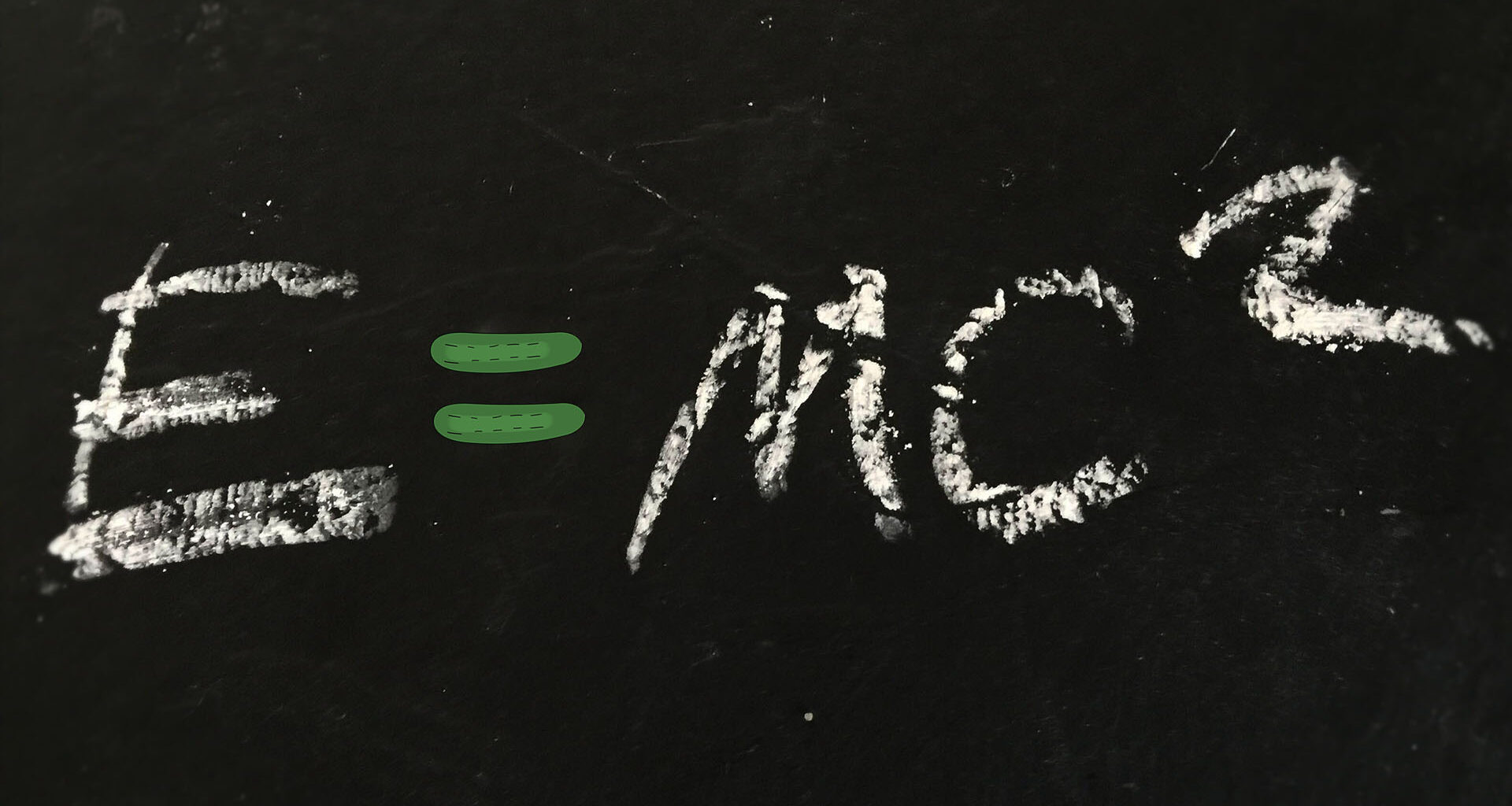Pytanie Ogórka: Znany wszystkim wzór E=mc² sugeruje równoważność masy i energii. Założenie proste nawet dla ogórka, ale czy powinienem traktować je absolutnie dosłownie? Czy potrafimy konkretnie stwierdzić ile energii kryje się w materii? I jaki mamy dowód na to, że natura rzeczywiście posługuje się tymi wielkościami jak dwiema wymienialnymi walutami?
Zaskakujący jest sam fakt, że jedno z najsłynniejszych twierdzeń w dziejach nauki zostało rzucone zupełnie niewinnie; jako uzupełnienie i dodatkowy wniosek, który przyszedł do głowy Alberta Einsteina już po opublikowaniu właściwej części szczególnej teorii względności.
W krótkim tekście sławny fizyk rozważył sytuację cząstki lub atomu, który poruszając się z pewną prędkością błyska, emitując fotony w dwóch przeciwległych kierunkach. Z punktu widzenia atomu, wyrzucone dokładnie w tym samym momencie fotony niczego nie zmieniają, bo ich “odrzut” ulega wzajemnemu zniesieniu. Ciekawszy jest natomiast punkt widzenia zewnętrznych obserwatorów, śledzących ruch atomu. Fala światła wylatującego “z tyłu” uciekającego obiektu okazuje się rozciągnięta i przesunięta ku czerwieni[1]. Z kolei drugi błysk wyemitowany w kierunku, do którego atom zmierza, będzie cechowało przesunięcie ku fioletowi i większa częstotliwość.
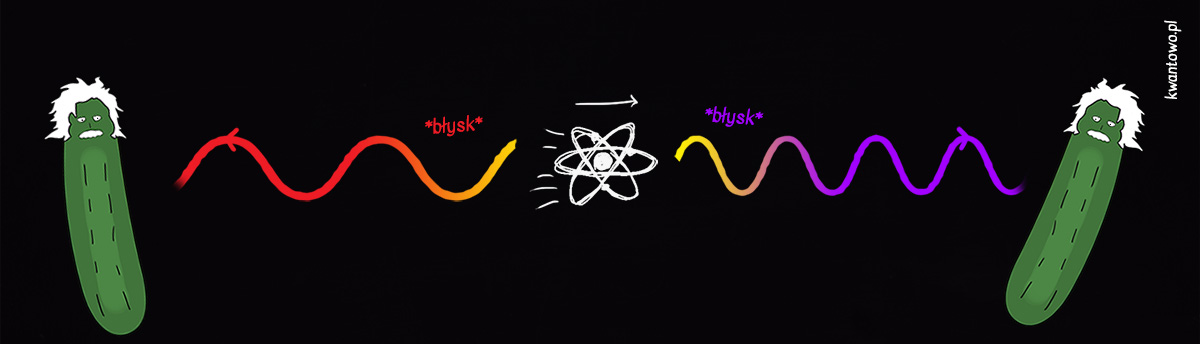
Tylko co z tego? Gdzie tu równoważność masy i energii?
Fotony mają zawsze identyczną prędkość, ale noszą różną energię i pęd[2]. W tym przypadku pierwszy foton ma mniejszą energię niż ten drugi. Gdybyśmy wypuścili nasz atom w pudle, oba błyski trafiłyby w przeciwległe ściany. Rzecz w tym, że błysk przesunięty ku fioletowi wywrze większe ciśnienie, niż ten słabszy przesunięty ku czerwieni. Pudło ulegnie popchnięciu przez jeden z fotonów. Właściwe pytanie brzmi: skąd wzięła się energia pozwalająca na to popchnięcie?
Z tego atomu, to oczywiste! Wciąż nie było tu słowa o masie.
Gdyby nie atom emitujący promieniowanie, na pewno nie doszłoby do pchnięcia pudła, ale wywołanie jakiegokolwiek fizycznego skutku wymaga zapłacenia określonej ceny. Bez względu na definicję, jedno o energii wiemy na pewno – musi zostać zachowana. W rejestrze przyrody bilans zawsze powinien wynosić zero. Nie można energii stworzyć, ani jej zniszczyć, a jedynie przekazać lub przekształcić. Tylko co może ulec przekształceniu w tej sytuacji? Poruszający się atom posiada w swoim fizycznym portfelu tylko dwie monety: wrodzoną masę i prędkość. W pierwszej kolejności należałoby założyć, że energia pochodzi z prędkości – pudło zostało popchnięte, a atom spowolniony. Przypominam jednak, że w opisanym eksperymencie obiekt wyrzuca z siebie dwa fotony w sposób absolutnie symetryczny, więc jego ruch pozostaje nienaruszony. Źródłem tajemniczej energii kopiącej pudełko musi być zatem druga dostępna moneta, czyli masa – odjęta od masy atomu[3].
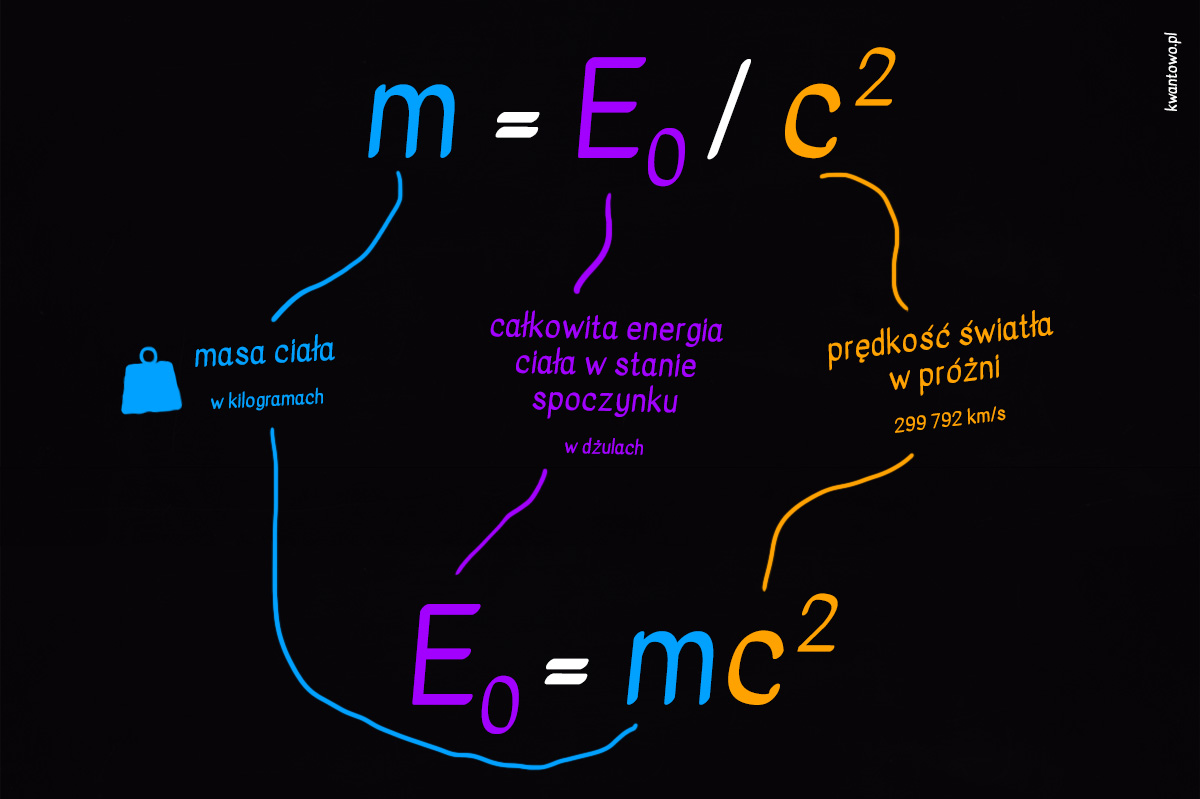
Dla współczesnego czytelnika może nie brzmi to zbyt szokująco, ale sto lat temu taki pomysł zwiastował prawdziwą rewolucję. Oto dochodzimy do wniosku, że masa ciała stanowi miarę zawartej w nim energii! Nawet Einstein w pierwszym odruchu nie był w stu procentach przekonany do tak nowatorskiej tezy. Pisał: “To zabawna i pociągająca myśl, ale zapewne dobry Bóg wyśmieje tę całą sprawę”. Nie musiało jednak minąć wiele czasu, aby rozczochrany uczony zrozumiał, że “zabawna myśl” ma odzwierciedlenie w rzeczywistości, a jej konsekwencje mogą być śmiertelnie (bardzo dosłownie) poważne.
Chwila, chwila, atom w pudełku to tylko jakiś eksperyment myślowy. Ale jeżeli mamy traktować tę teorię dosłownie, to wszystkie obiekty wypromieniowując energię tracą masę – i odwrotnie – kiedy energię otrzymują to stają się masywniejsze. Przecież tak się nie dzieje.
Ależ dokładnie tak się dzieje, tyle że w zdecydowanej większości przypadków ten efekt jest tak mikroskopijny, że nawet dzisiaj niełatwo nam go zmierzyć. Kiedy wlejesz litr wody do czajnika i doprowadzisz ją do wrzenia (co będzie wymagało jakichś 400 tys. dżuli energii), jej masa wzrośnie o kilka miliardowych części grama.
Mówi nam to dwie rzeczy. Po pierwsze, trzeba zainwestować niesamowicie dużo energii żeby odnotować widoczny wzrost masy układu. Po drugie, patrząc na sprawę odwrotnie, z niewielkiej ilości masy teoretycznie można wydobyć bezlik energii.
Pewnie dlatego, tezy Einsteina stały się podstawą działania broni jądrowej.
Przykłady działania E=mc² otaczają nas bez przerwy. Kiedy bryłka uranu lub innego ciężkiego pierwiastka emituje promieniowanie, wiąże się to z nieustannym, delikatnym ubytkiem jej masy. Oświetlające i grzejące naszą planetę Słońce, czerpiąc energię z procesu fuzji termojądrowej, w każdej chwili chudnie o kilka milionów ton.
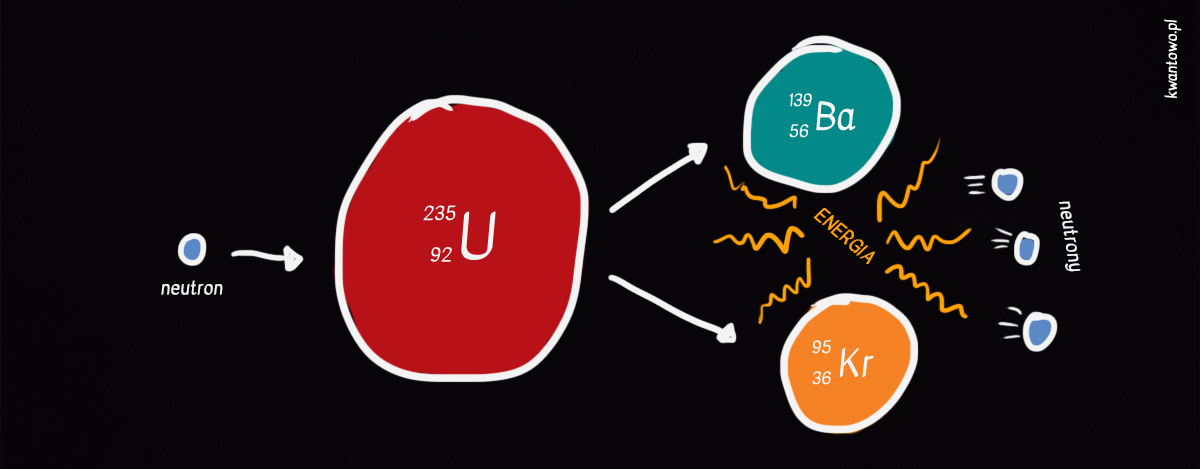
Reakcja łańcuchowa leżąca u podstawy konstrukcji bomby jądrowej również nie jest tu wyjątkiem. Zresztą był to jeden z pierwszych poważnych testów myśli Einsteina. Do pionierskiego rozbicia jądra atomu doprowadzono w przedwojennych Niemczech, podczas doświadczenia polegającego na bombardowaniu uranu swobodnymi neutronami. Wynik okazał się nietypowy: rozszczepione jądro uranu rozpadało się na jądra baru i kryptonu, które razem “ważyły” ciut mniej niż pierwotnie uran. Fizycy natychmiast zrozumieli, że zaobserwowali ubytek masy przewidziany przez Einsteina. Masy transformowanej w solidną porcję energii.
A czy masę ogórka lub człowieka możemy przeliczyć na energię?
Teoretycznie tak. Żeby wyliczyć tę “energię istnienia” należy przemnożyć masę ciała przez prędkość światła w próżni do kwadratu. Prędkość światła wynosi 300 000 km/s, toteż wynik takiego mnożenia jest bardzo wysoki. Jeżeli przyjmiemy, że przeciętny ogórek waży 200 g, to więzi on w sobie 18 biliardów dżuli energii[4], co wystarczyłoby do zdemolowania Hiroszimy 280 razy.
Jednak zamiana 100% materii w energię jest nieprawdopodobna. Tylko drobny procent paliwa jądrowego faktycznie zostaje przekształcony w energię, co i tak wystarcza do spowodowania niszczycielskiego wybuchu lub zasilenia elektrowni. Najbardziej wydajnym procesem fizycznym pozwalającym zamienić masę w energię wydaje się anihilacja, która następuje podczas spotkania cząstki z jej antycząstką. Kiedy ujemnie naładowany elektron wpada na pozyton – swoje dodatnio naładowane alter ego – kończy się to wzajemnym unicestwieniem w miniaturowym błysku promieni gamma[5]. Jeśli więc zechcemy uwolnić wspomniane biliardy dżuli z ogórka, musimy go skonfrontować z jakimś antyogórkiem. Nie wiem jednak gdzie takie rosną.
Znam tę zasadę: jeżeli spotkasz swojego brata bliźniaka zbudowanego z antymaterii, nigdy nie podawaj mu ręki. Wygląda na to, że materia to taki niewykorzystany rezerwuar energii.
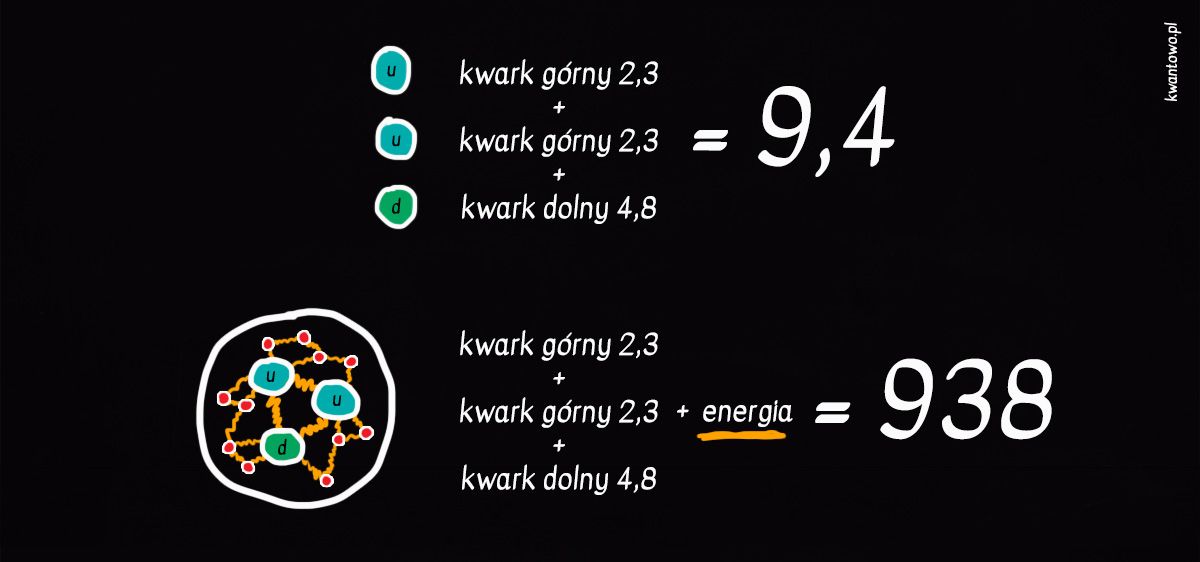
Nasza współczesna wiedza o materii dodaje temu twierdzeniu dodatkowego smaczku. Mianowicie, kiedy piszę o tym, że materia kumuluje lub więzi w sobie energię, nie stosuję żadnej metafory. Zdecydowana większość, bo ponad 90% masy budujących nas atomów, to emanacja wielkiej energetycznej burzy, rozgrywającej się wewnątrz jąder. Gdybyś zajrzał do wnętrza protonu lub neutronu, znalazłbyś skomplikowany mechanizm oparty o tercet kwarków wymieniających się mniejszymi gluonami oraz cząstkami wirtualnymi. Sztuczka polega na tym, że masa własna trzech zsumowanych kwarków wynosi niecałe 10 MeV[6], podczas gdy cały proton “waży” prawie 940 MeV. Za taki rezultat odpowiada właśnie energia, zwłaszcza energia wiązań oraz energia kinetyczna towarzysząca ruchliwym cząstkom zamieszkującym jądro każdego atomu.
Materia naszych ciał naprawdę kipi od zamkniętej w niej energii. Nie różnimy się pod tym względem od wspomnianego czajnika z gorącą wodą. Tyle, że rolę rozedrganych molekuł H2O pełnią w tym przypadku dynamiczne kwarki i gluony.