Wszystko co może zostać wypromieniowane, zostaje wypromieniowane.
Richard Price
Kosmiczne zakola
Natura na ogół rozpieszcza nas różnorodnością. Spójrzmy na planety. Każda stanowi osobny świat, który moglibyśmy opisywać godzinami, analizując jego wielkość, pole magnetyczne, geologię, temperaturę i strukturę powierzchni, gęstość i skład atmosfery, obecność pierścieni i tak dalej. Rozprawiając o gwiazdach, zwrócimy uwagę na stadium ewolucji, barwę, plamy, protuberancje, jasność i jej wahania. Oczywiście katalogujemy ciała niebieskie, wyławiając ich podobieństwa (gazowe olbrzymy, galaktyki spiralne, czerwone karły itd.), ale bez wątpienia każdy obiekt jest na swój sposób unikatowy. Jeśli się postaramy, zawsze znajdziemy jakąś cechę rozpoznawczą; coś w rodzaju kosmicznego odcisku kciuka.
A co powiemy o przykładowej czarnej dziurze? Załóżmy, że kierujemy statkiem kosmicznym zawieszonym w przestrzeni nad mroczną taflą horyzontu zdarzeń. Czy również potrafilibyśmy wymienić jakiś wyróżnik charakterystyczny dla tego jednego, konkretnego obiektu? A może mamy do czynienia z astrofizycznymi klonami dzielącymi tę samą złowieszczą twarz, niczym matrixowy Agent Smith?
Fizycy, którym przyświecała ta myśl, zaczęli powtarzać za wielkim Johnem Archibaldem Wheelerem[1], że “czarne dziury nie mają włosów”. Trudno powiedzieć, co naprowadziło amerykańskiego teoretyka na ten fryzjerski aforyzm, ale trzeba przyznać, że oddaje on istotę rzeczy w bardzo obrazowy sposób. Włosy stanowią tu oczywiście metaforę fizycznych właściwości, pozwalających na zidentyfikowanie danego obiektu. Idąc tym tropem powiedzielibyśmy, że dowolna planeta, gwiazda, mgławica, księżyc czy planetoida, nosi całkiem bujną czuprynę. Czarna dziura natomiast, dokładnie odwrotnie, pozostaje prawie łysa, zaś wszystkie metaforyczne włosy można zliczyć na palcach jednej ręki.
Włos masy
Włos numer jeden dotyczy najbardziej oczywistej właściwości czarnej dziury: jej masy i ściśle sprzężonych z nią rozmiarów. Promień horyzontu zdarzeń dla przeciętnej, gwiazdowej czarnej dziury o masie 10 Słońc (M⊙) wynosi zaledwie 30 kilometrów, ale już dla supermasywnego Sagittariusa A* z centrum Drogi Mlecznej, będzie to ponad 12 milionów kilometrów. Przyznacie, że trudno byłoby przeoczyć taką dysproporcję i pomylić oba obiekty. Załóżmy jednak, że przymykamy oko na skalę. Czy pomijając rozmiary, nadal bylibyśmy w stanie dokonać rozróżnienia? Czy na nieprzeniknionej powierzchni horyzontu zdarzeń nie dałoby się dostrzec jakichś charakterystycznych odkształceń? Kto w ogóle powiedział, że czarna dziura musi koniecznie przyjmować formę doskonałej sfery?
Karl Schwarzschild i inni pionierzy badań nad czarnymi dziurami, snuli swoje wczesne rozważania w oparciu o maksymalnie uproszczony model. Dla ułatwienia zakładano scenariusz kolapsu doskonale kulistej, statycznej gwiazdy o symetrycznym polu grawitacyjnym, rodzącej równie nieskazitelny, sferyczny horyzont zdarzeń. Problem polega na tym, że realne obiekty zazwyczaj znacznie odbiegają od ideału.
Co jeśli umierająca w konwulsjach gwiazda okaże się zdeformowana, a na jej powierzchni ujawni się wyraźne wybrzuszenie? Takie aberracje zdarzają się w rzeczywistości, czego dowiodły chociażby obserwacje Betelgezy. Czy w takim przypadku otrzymamy garbatą czarną dziurę? Pójdźmy jeszcze o krok dalej. Wyobraźmy sobie, że potrafimy poddać kolapsowi grawitacyjnemu kostkę Rubika – czy hipotetyczny horyzont zdarzeń przybrałby kanciastą formę sześcianu?
Rozwiązanie tej zagadki zawdzięczamy wyjątkowo nie amerykańskim naukowcom, lecz przede wszystkim kreatywności złotego pokolenia radzieckich astrofizyków – Jakowa Zeldowicza, Igora Nowikowa, Andrieja Doroszkiewicza – oraz urodzonego w Berlinie i pracującego w Kanadzie Wernera Israela. Teoretycy doszli do wniosku, że w rachubę wchodzą dwie możliwości. Albo każda deformacja na ciele gwiazdy, bez względu na jej wielkość, wywołuje szybko rosnące, niekontrolowane zniekształcenie czasoprzestrzeni; albo umierająca gwiazda, mimo wszystko, zawsze formuje doskonale sferyczny horyzont zdarzeń. Druga propozycja była pod każdym względem lepsza, ale wymagała wynalezienia naturalnego mechanizmu zdolnego do wygładzania powierzchni kolapsujących obiektów.
Przyjęto następujące rozumowanie. Kiedy niesymetryczna gwiazda ulega ściskaniu do promienia krytycznego, nowoutworzony horyzont zdarzeń nawet jeśli dziedziczy deformację, to tylko przez moment. Przykładowy garb gwiazdy kryje się pod horyzontem, więc przestaje wywierać wpływ na powierzchnię czarnej dziury, która natychmiast dąży do sprasowania i wygładzenia. Kip Thorne w plastyczny sposób porównał ten proces do szarpania struny gitary. Kiedy puszczamy strunę, ta powraca do naturalnego położenia, przy okazji drgając i posyłając w przestrzeń fale dźwiękowe. Znikające deformacje na powierzchni czarnej dziury również pozostawiają ślad, marszcząc tkankę pobliskiej czasoprzestrzeni i emitując w kosmos fale grawitacyjne[2].
Wniosek jest taki, że horyzont zdarzeń statycznej czarnej dziury może posiadać przeróżne rozmiary, ale poza tym w każdym przypadku pozostaje gładką, łysą sferą. Nie szpecą jej żadne wzniesienia, doliny, kratery, fałdy, kanty, rowy, ani inne rodzaje geometrycznych włosów.
Włos elektromagnetyzmu
W tym samym czasie inny radziecki fizyk, przyszły noblista i właściciel imponujących krzaczastych brwi – Witalij Ginzburg – dumał nad czarnymi dziurami w kontekście elektromagnetyzmu. W pierwszej kolejności interesowało go, czy czarna dziura zachowuje pole magnetyczne, jeżeli takowe posiadała kolapsująca gwiazda. Obliczenia i prymitywne komputerowe symulacje wskazywały, że wraz z kurczeniem ciała, natężenie pola powinno wzbierać na sile (zmniejszenie rozmiarów o połowę zwiększa pole magnetyczne czterokrotnie), aby po osiągnięciu przezeń promienia krytycznego, skoczyło do nieskończoności. Po raz kolejny należało przyjąć, że albo natura pozwala sobie na niedorzeczne wyniki, albo umierająca gwiazda gubi gdzieś po drodze magnetyczne włosy. Po latach udało się naszkicować model zgrabnie współgrający z drugą opcją.
Aby zrozumieć tę koncepcję, musimy sobie przypomnieć, że źródło pól magnetycznych ciał niebieskich, tkwi w ich wnętrzach. W przypadku planet (jak Ziemia) może być to efekt geodynama napędzanego przez prądy konwekcyjne płynnego jądra; w przypadku gwiazd bardziej złożone przepływy rozgrzanej plazmy. W każdym przypadku, linie pola magnetycznego są generowane i zakorzenione gdzieś wewnątrz obiektu. W momencie gdy miażdżona gwiazda formuje horyzont zdarzeń, pole ulega natychmiastowemu odcięciu od źródła. Dlatego magnetyczne włosy ulatują w przestrzeń kosmiczną, transformując w postać fal promieniowania elektromagnetycznego.

Te same wnioski nie dotyczą natomiast ewentualnego ładunku elektrycznego czarnej dziury. Na początku może wydać się to dziwne, ale gdyby umierająca gwiazda nosiła ładunek dodatni bądź ujemny, powstała z niej dziura również byłaby obdarzona ładunkiem dodatnim lub ujemnym. Linie pola elektrycznego rozchodzą się radialnie wokół obiektu, są skierowane na zewnątrz i nie wymagają zakotwiczenia pod powierzchnią horyzontu zdarzeń (w odróżnieniu od linii pola magnetycznego). Istnieje również inny, głębszy powód takiego stanu rzeczy. Ładunek elektryczny należy do elitarnego grona wielkości fizycznych, które nigdy, pod żadnym pozorem nie mogą sobie ot tak po prostu wyparować. Zakazują im tego fundamentalne prawa zachowania.
Oznacza to, że fizyka jak najbardziej dopuszcza istnienie czarnych dziur obdarzonych włosem określonego ładunku elektrycznego.
Należy jednak podkreślić, że jest to włos teoretyczny, albowiem wszystkie lub niemal wszystkie znane nam obiekty astronomiczne pozostają elektrycznie neutralne. A skoro i tak nie posiadają dodatniego czy ujemnego ładunku, to nie mają nic do przekazania czarnej dziurze.
Włos obrotu
Bardziej realną wartością, którą natura również nakazuje sztywno zachowywać, jest moment pędu. We wszechświecie wszystko wiruje, włącznie z olbrzymimi gwiazdami, które umierając, całą energię ruchu obrotowego przepisują swoim niewielkim spadkobiercom. Najlepszy przykład stanowią pulsary, zdolne do wykonywania setek obrotów wokół własnej osi na sekundę. Czarne dziury powstają w zbliżonych okolicznościach, mamy więc pełne prawo zakładać, że i one wirują. Niewykluczone nawet, że okazałyby się w tych piruetach żwawsze od swoich kuzynów[3].

Ruch obrotowy, choć nie brzmi zbyt ekscytująco czy skomplikowanie, zmienia niemal wszystko. Osobliwość nie jest już punktem, lecz czymś na kształt obwarzanka lub krążka. Horyzont zdarzeń ulega spłaszczeniu na biegunach i wybrzuszeniu w okolicach równika[4], analogicznie do naszej planety. Wreszcie, wirowanie wywołuje w okolicy horyzontu silny efekt wleczenia czasoprzestrzeni, nie bez przyczyny porównywany do grawitacyjnego tornada. Każda cząstka porwana przez ten wir musi obiegać czarną dziurę i nie może się zatrzymać. Nadal posiada fizyczną możliwość ratunku i ewakuacji na zewnątrz (w odróżnieniu od wnętrza horyzontu zdarzeń), ale geometria czasoprzestrzeni wyklucza stan spoczynku. Obszar ten, nazywany ergosferą, towarzyszy wyłącznie wirującym czarnym dziurom, a jego rozmiary rosną wraz z tempem rotacji.
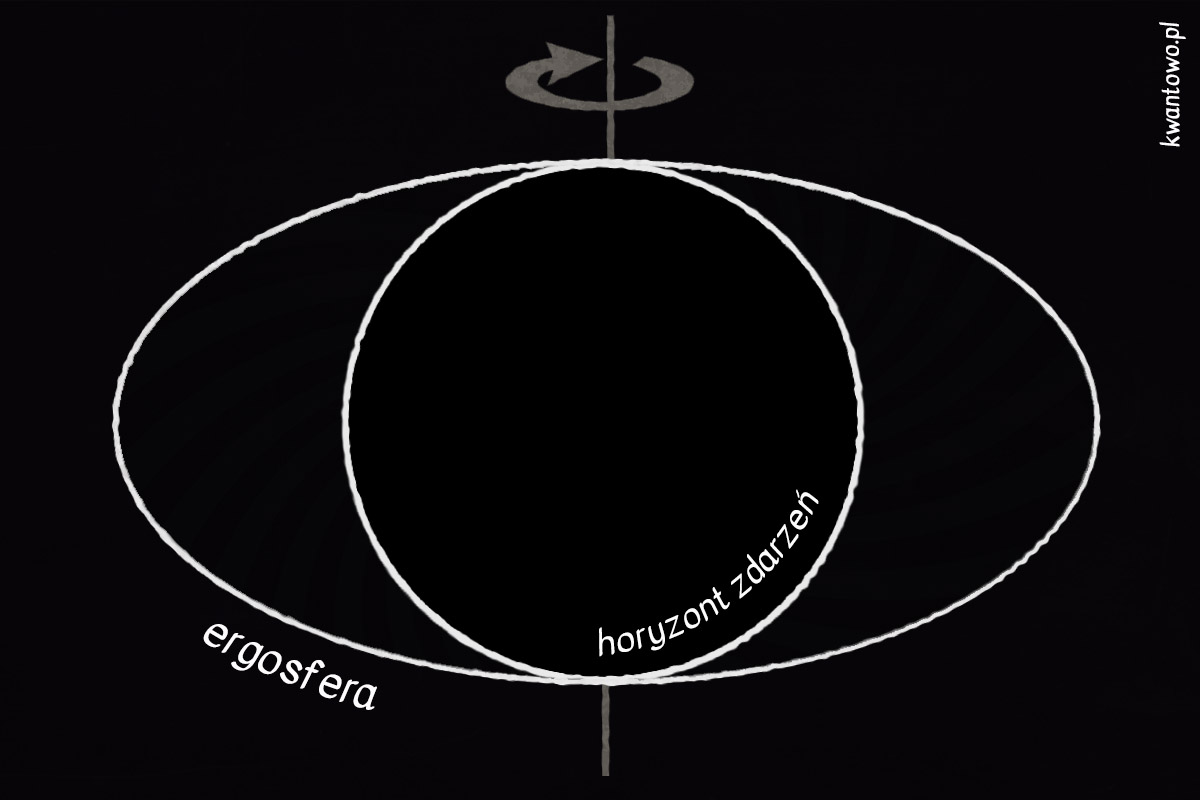
Elegancka prostota
Zgodnie z powyższym, do sporządzenia pełnego fizycznego opisu czarnej dziury wystarczy wyznaczyć jej masę, moment pędu oraz (ewentualnie) ładunek elektryczny. Tylko trzy, a w praktyce dwie wielkości decydują o tożsamości obiektu, podczas gdy wszystko inne przykrywa koc horyzontu zdarzeń albo ulatuje w przestrzeń. Koszmar literata.
Czyni to czarną dziurę bardzo egzotyczną, ale zarazem niesłychanie prostą strukturą; pod wieloma względami bliższą cząstkom subatomowym niż innym obiektom astronomicznym. Amerykański fizyk Richard Price zauważył, że zapadająca gwiazda pozostawia sobie tylko to, czego fizycznie nie jest w stanie w żaden sposób się pozbyć. Swoją myśl skondensował do błyskotliwego zdania: “Wszystko co może zostać wypromieniowane, zostaje całkowicie wypromieniowane”.

Ale czy to oznacza, że katalog włosów należy uznać za ostatecznie zamknięty? Niekoniecznie. Niemal co roku pojawia się publikacja przekonująca, że czarne dziury mogą skrywać jeszcze jakiś znak rozpoznawczy. Najczęściej są to jednak hipotezy odnoszące się tylko do określonego typu czarnych dziur, albo mające zastosowanie wyłącznie w bardzo specyficznych, nierzadko nierealnych warunkach. Jednak nawet takie, pozornie naiwne rozważania są cenne, bo mówią nam wiele o istocie struktury czasoprzestrzeni.
Jednak co do zasady John Wheeler miał rację. Czarna dziura, pozostaje bardzo prosta i tak łysa, na ile to tylko możliwe.










