Gdy czas był przestrzenią: Model Hawkinga-Hartle’a

Sądzę, że dla następnego pokolenia te koncepcje staną się równie naturalne jak fakt, że Ziemia jest okrągła.
Stephen Hawking

Niepojęty wielki wybuch

Ludzki umysł nie jest przystosowany do rozmyślania o warunkach, w których nie ewoluował i których nigdy nie doświadczył. Spróbuj sobie wyobrazić, drogi Czytelniku, dodatkowy wymiar przestrzenny. Albo kompletny brak przestrzeni. I w końcu, podejmij próbę wyobrażenia sobie rzeczywistości pozbawionej czasu. To niełatwe, jeśli nie niemożliwe. Fizycy wspomagają się w takich sytuacjach matematyką oraz różnorakimi sztuczkami, ale co do zasady nasze mózgi dostają paraliżu, gdy zostają postawione przed kategoriami absolutnie oderwanymi od codziennych doświadczeń.

Fakt ten niezawodnie utrudnia ludziom zrozumienie oraz akceptację abstrakcyjnych teorii naukowych, a właśnie do takowych uciekamy się, opisując początki wszechrzeczy. Mówimy o procesach, które zrodziły nie tylko całą istniejącą materię i energię, ale również wykreowały samą czasoprzestrzeń. Rozważając tę myśl, w naturalnym odruchu zaczynamy zadawać standardowe pytania: “Jak powstało coś z niczego?”, “Gdzie nastąpił wielki wybuch?”, czy wreszcie “Co było przed wielkim wybuchem?”. Zatrzymajmy się przy tym ostatnim dylemacie. Od niemal stu lat zdajemy sobie sprawę, że współczesny wszechświat podlega nieustannej ekspansji. Przestrzeń puchnie, galaktyki od siebie uciekają, materia ulega rozrzedzeniu. Oznacza to równocześnie, iż cofając się po linii czasu, dostrzeglibyśmy zjawisko odwrotne. W przeszłości gabaryty wszechświata prezentowały się znacznie skromniej, zaś wszystkie elementy naszego nieboskłonu – widzialne oraz niewidzialne, dobrze znane jak i jeszcze nieodkryte – znajdowały się znacznie bliżej siebie niż obecnie. Cofając się w ten sposób coraz bardziej i bardziej, nieuniknione staje się dotarcie do momentu zero. Zdrowy rozsądek każe nam wyciągnąć wniosek, że 13 miliardów 820 milionów lat temu komplet składników wszechświata – całość kosmicznej energii i wszystkie cząstki elementarne – były skumulowane w jednym punkcie. Ojciec teorii wielkiego wybuchu, Georges Lemaître, ochrzcił ten obiekt mianem pierwotnego atomu, choć współcześni badacze wolą mówić o osobliwości.

Punkt zero

Wszystko, o czym teraz rozprawiamy, można sprowadzić do pojęcia warunków początkowych lub, jak kto woli, warunków brzegowych. Chodzi po prostu o pewną sytuację panującą na starcie określonego procesu fizycznego. Jeżeli badałbym przebieg wystrzelenia pocisku z katapulty, interesowałaby mnie masa kamienia, siła ziemskiego przyciągania, kierunek wiatru, długość ramienia wyrzutni, stosunki naprężenia lin, sprężyn i tak dalej. To byłyby warunki brzegowe dla strzału z katapulty. Znając je wszystkie, przy wykorzystaniu standardowych reguł fizyki klasycznej, dałoby się z ogromną precyzją przewidzieć tor lotu głazu. Działa to też w drugą stronę: na podstawie obserwacji frunącego pocisku możemy pokusić się o opisanie warunków brzegowych, jakie doprowadziły do jego wystrzelenia.

Ewolucja wszechświata nie jest pod tym względem wyjątkowa. To monstrualne doświadczenie fizyczne, w którym chcąc nie chcąc wszyscy bierzemy udział. Rozważania o osobliwości są zatem niczym innym niż poszukiwaniem warunków brzegowych dla obserwowanego rozszerzania kosmosu.

Jak już wcześniej stwierdziliśmy, wiele wskazuje na fakt, iż u zarania wszystko, co znamy było upakowane w jednym, ekstremalnie gorącym i gęstym punkcie. Sam pomyśl: jakie obrazy podsuwa Ci Twój umysł kiedy czytasz o big bangu i pierwotnej osobliwości? Większość z nas mimowolnie myśli teraz o punkcie, o kropce, o jakiejś drobinie, może nawet namacalnej. A skoro mamy do czynienia z konkretnym, klarownym punktem – z wytworem naszego schematycznego rozumowania – to zadajemy równie schematyczne pytania. Chcemy wiedzieć, skąd ten punkt się wziął, dlaczego zaczął się zmieniać, gdzie się znajdował i naturalnie, co było przed nim. To sensowne, bo funkcjonujemy w realiach o jasno sprecyzowanych zasadach, wedle których każdy skutek poprzedza jakaś przyczyna. Hipotetyczny brak czasu oznaczałby brak związków przyczynowo-skutkowych, ergo brak jakichkolwiek zmian. Bez tykającego zegara, “coś” nie mogło nagle “wybuchnąć”. Wszystko staje na głowie, a nasza wizja logicznie spójnego świata chwieje się w posadach. Prosta osobliwość, będąca ostrym punktem na wykresie, zamyka nas w labiryncie pułapek myślowych.

A co jeśli nasze założenia dotyczące warunków brzegowych są mylne? Co jeśli nigdy nie było żadnego punktu zero? Co jeśli osobliwość przybrała zupełnie inną formę? Co jeśli wszechświat zrodził się w wielkim wybuchu, ale moment startu wyglądał znacznie, znacznie ciekawiej od tego co podsuwa nam intuicja?

Warunki brzegowe? Brak brzegu!

Przez dekady teoretycy z lękiem zerkali na problem warunków brzegowych wielkiego wybuchu. Owszem, wielu z zacięciem publikowało prace odnoszące się do wszechświata w wieku niemowlęcym, sięgając obliczeniami do ułamka sekundy po wielkim początku. Jednak sama osobliwość stanowiła temat tabu. Była czymś, co ze swej natury leżało poza możliwością poznania. Właśnie dlatego społeczność naukowa z oszołomieniem przyjęła śmiałą szarżę dwóch błyskotliwych czterdziestolatków, którzy w artykule Funkcja falowa wszechświata z 1983 roku uderzyli wprost w osobliwość. Nie w pierwszą sekundę po narodzinach wszechświata, nie setną część sekundy, nie miliardową część sekundy – interesował ich sam moment startu.

Tymi uczonymi byli James Hartle (w niebieskiej koszuli na poniższej fotografii) z Uniwersytetu Kalifornijskiego oraz zmarły niedawno Stephen Hawking, sprawujący profesurę w Cambridge. (Na marginesie, nie ukrywam, że jedną z moich głównych motywacji do napisania artykułu było przybliżenie szerszej widowni jednego z dwóch – obok hipotezy promieniowania czarnych dziur – gigantycznych osiągnięć brytyjskiego profesora. Jeśli więc nie zdawałeś sobie sprawy, z czego wynikał ogromny szacunek świata nauki do Hawkinga, postaraj się dotrwać do końca tego tekstu).

Hipoteza Hartle’a i Hawkinga na temat warunków początkowych była szokująca, tym bardziej że zakładała… brak początku. A ściślej mówiąc brak “ostrego” początku, kompletne wyrzucenie z rozumowania ściśle określonego punktu startowego. Miał być to wszechświat pozbawiony brzegów. Co więcej, fizycy przekonywali, że taki model wielkiego wybuchu jest nie tylko prawdopodobny, ale jako jedyny współgra z regułami wytyczonymi przez mechanikę kwantową. Żeby zrozumieć, dlaczego to tak istotny element układanki, musimy na chwilę zostawić wielki kosmos i zanurzyć się w rzeczywistość subatomową.

Nieoznaczona osobliwość

Wkraczając niepewnym krokiem w kwantową dżunglę, prędko orientujemy się, że nic nie jest tu takie jak w wizjach Galileusza, Newtona i Einsteina. Mikroświat pozostaje osadzony na trudnym do ogarnięcia fundamencie, znanym każdemu amatorowi fizyki pod nazwą zasady nieoznaczoności Heisenberga. Słynny niemiecki naukowiec dostrzegł, że cząstki elementarne nie mogą zachowywać się zgodnie z zasadami mechaniki klasycznej i ukuł fenomenalne, choć zarazem wywrotowe twierdzenie: znając ściśle określone położenie cząstki, tracimy wiedzę o jej pędzie, a poznając pęd, umyka nam informacja o jej położeniu. Nie istnieje elektron, kwark czy neutrino o dokładnie zdefiniowanym położeniu i pędzie. Każdy obiekt o rozmiarach subatomowych przybiera widmową formę, pokornie znosząc dyktat zasady nieoznaczoności.

Każdy. Zatem, czy to oznacza, że pierwotna osobliwość kumulująca całą zawartość wszechświata, również pozostawała nieokreślona?

Dokładnie takie założenie poczynili Hawking i Hartle. Jeżeli upatrujemy początek rzeczywistości w czymś skrajnie małym, to siłą rzeczy mamy święty obowiązek uwzględnić rygory mechaniki kwantowej. Niesie to za sobą szalenie istotne konsekwencje. Mikroskopijna osobliwość podlegała prawu nakreślonemu przez Heisenberga, co oznacza, że nie mogła posiadać jednocześnie zdefiniowanego pędu i położenia. Wyobrażenie wyraźnej drobiny, która zrodziła wszechświat musimy wybić sobie z głowy. Ale to dopiero początek.

Musisz wiedzieć – co wiele opracowań pomija – że zasada nieoznaczoności obejmuje znacznie więcej zjawisk niż tylko ruch i położenie cząstki. W rzeczy samej nieokreśloność dotyczy różnych par komplementarnych wielkości. W artykule poświęconym naturze próżni i fluktuacjom kwantowym, opowiadałem o podobnej relacji czasu i energii. W każdym momencie, wszędzie wokół nas dochodzi do spontanicznego powstawania cząstek wirtualnych, co jest nie tylko umożliwiane, ale wręcz wymagane przez regułę Heisenberga. Próżnia posiada potencjał do kreowania na krótką chwilę par elektron-pozyton, ponieważ energii próżni i czasu życia fluktuacji rónież nie da się określić z dowolną dokładnością.

Nasi bohaterowie poszli o krok dalej i pokusili się o kolejny pomysł na wykorzystanie właściwości fizyki kwantowej. Zgodnie z ich propozycją, w młodym i skurczonym wszechświecie, zasadzie nieoznaczoności podlegała sama czasoprzestrzeń.

Czas urojony Hartle’a i Hawkinga

Czas realny i czas urojony na układzie współrzędnych

Pozwól, że nie będę w tym miejscu rozpoczynał żadnych głębszych refleksji nad definicją czasu, i pozostanę przy jego prostym ujęciu jako czwartego wymiaru, pozostającego w stałym związku z trzema wymiarami przestrzennymi. W modelu Hawkinga-Hartle’a, przestrzeń i czas stanowią parę wartości nieokreślonych, nie inaczej niż pęd i położenie przykładowego elektronu. Pierwotna osobliwość przybiera formę kwantowej fantasmagorii, w której czas nabiera cech przestrzeni i wraz z energetyczną zawartością, nie może zostać opisany bez uwzględnienia zasady nieoznaczoności oraz równań falowych. Istne szaleństwo, niemające nic wspólnego z tym co podpowiadają nam zmysły i intuicja.

Od strony matematycznej, dla skonstruowania czasu urojonego duet H-H posłużył się liczbami urojonymi.

Dodatek: O co chodzi z liczbami urojonymi?

Liczby urojone stanowią szczególny przypadek liczb zespolonych. Ich genezy należy szukać w wieku XVI, kiedy to Niccolò Fontana (znany jako Tartaglia), a później Girolamo Cardano, próbowali efektywnie rozwiązywać równania wielomianowe trzeciego stopnia. Ten drugi (znany również z obecnego w każdym samochodzie przegubu Cardana) napotkawszy konieczność pierwiastkowania liczb ujemnych, poszedł za ciosem. Nagrodą było to, że w ostatecznym rozrachunku pierwiastki z liczb ujemnych znikły.

Współcześnie liczbami zespolonymi nazywamy liczby postaci a+bi, gdzie a,b są zwykłymi liczbami rzeczywistymi, zaś i jest tzw. jednostką urojoną, tzn. i²=-1. Liczbę a nazywamy częścią rzeczywistą, zaś liczbę b częścią urojoną liczby zespolonej a+bi. Dlatego liczby rzeczywiste (dla których b=0) stanowią podzbiór zbioru liczb zespolonych. Innym podzbiorem są liczby urojone, dla których a=0. Współcześnie liczby zespolone znajdują zastosowanie w wielu działach matematyki i techniki (algebra, analiza matematyczna, analiza funkcjonalna, elektrotechnika) oraz, jak widać, w fizyce i kosmologii.

Gościnnie: Szymon Wąsowicz z bloga Byc-Matematykiem.pl

Weźmy za przykład wyrażenie 3². Wartość tego potęgowania wynosi oczywiście 9. A jakie będzie rozwiązanie dla wyrażenia (-3)²? Również 9. W krainie liczb urojonych sprawa wygląda jednak inaczej: urojona trójka do kwadratu daje -9 (a właściwie (3i)²=9i²=-9, po więcej odsyłam do gościnnej ramki powyżej). Nietrudne, chociaż rzecz jasna sam sposób wykorzystania tej idei w publikacji z 1983 roku był dalece mniej zrozumiały dla nie-matematyków. W każdym razie, sztuczka polegająca na mnożeniu współrzędnych czasowych przez liczby urojone, doprowadziła do rzeczy niebywałej. Czas można było traktować w równaniach dokładnie tak samo jak przestrzeń. W miejscu einsteinowskiej, czterowymiarowej czasoprzestrzeni pojawia się prostsza struktura złożona wyłącznie z czterech wymiarów przestrzennych!

Czujesz się skołowany? Przypomnijmy więc do tego, że w tę całą poskręcaną geometrię wtrącono jeszcze smaczek pod postacią reguł mechaniki kwantowej.

Gładki początek

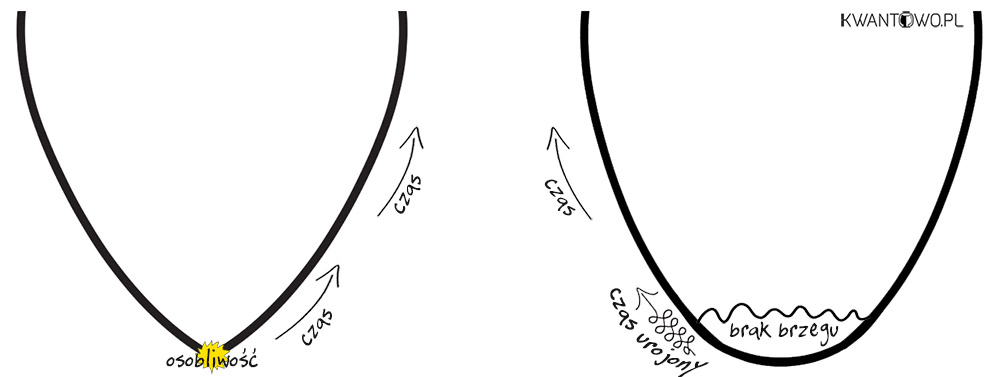
Zauważ jak mocno powyższa hipoteza przemeblowuje nasze podejście do początku wszechrzeczy. Zgodnie z modelem Hartle’a-Hawkinga nigdy nie było żadnej punktowej osobliwości, lecz kwantowy geometryczny chaos. Warunkiem brzegowym dla wczesnego wszechświata był… brak brzegu. Wszechświat nie jest nieskończony, posiada swoje ramy, ale nie posiada krawędzi – trochę jak Kula Ziemska. Myślę, że najłatwiej uchwycić to na grafice (patrz niżej). “Stare” ujęcie narodzin wszechświata z pierwotnej osobliwości, na prostym wykresie przybrałoby formę zwykłego stożka. Wyraźny wierzchołek symbolizuje nagłe przejście ze stanu nicości w stan istnienia. Czasoprzestrzeń po prostu się pojawia i z miejsca ekspanduje. W modelu Hartle’a-Hawkinga ostra osobliwość zupełnie znika zastąpiona przez charakterystyczne miękkie zaokrąglenie. Czas był tożsamy z przestrzenią, więc u spodu nie uświadczymy punktu zero, lecz gładkie zasklepienie. To niewyraźny stan, w którym – jak to elegancko ujmuje w swojej książce Michał Heller – dzięki regułom kwantowym istniało tylko pewne prawdopodobieństwo złamania symetrii i trwałego wyodrębnienia wymiaru czasowego. Dopiero kiedy wskazówka nieoznaczoności zaliczyła pierwsze tyknięcie wybijając magiczne 10^-44 sekundy, mogło rozpocząć się kształtowanie znanej nam, stabilnej czasoprzestrzeń.

Model wielkiego wybuchu Hartle'a i Hawkinga

Później wydarzenia potoczyły się już lawinowo. W ułamku sekundy doszło do serii kolejnych pęknięć w przedwiecznej symetrii: powstało zjawisko masy, cztery oddziaływania podstawowe i pierwsze cząstki elementarne. Po kilku sekundach kwarki złączyły się w protony i neutrony, które po trzech minutach uformowały ogromne ilości jąder atomowych. Po setkach tysięcy lat chmury wodoru i helu uległy zmiażdżeniu przez wszechwładną grawitację, powołując do istnienia protogwiazdy i zalążki galaktyk. Około 10 miliardów lat później, na planecie krążącej wokół jednej z takich gwiazd doszło do narodzin życia, które w drodze długotrwałej ewolucji pozwoli na wykiełkowanie świadomości.