Po pierwsze, zrób masę.
Anonimowy fizyk na siłowni
Wszyscy robimy to źle
Mam nadzieję, że nie obrazisz się drogi Czytelniku, jeśli na wszelki wypadek zacznę od informacji elementarnych. Nie wątpię, że większość z nas doskonale pamięta z czasów szkolnych, na czym polega różnica między masą i ciężarem. Jednakże doświadczenie podpowiada, że zawsze istnieje pewien odsetek odbiorców, których pamięć jest równie ulotna co marsjańska atmosfera. A trudno rozmawiać o kilogramie, bez wiedzy o tym, jaką wielkość on właściwie reprezentuje.
Interesującym nas dziś terminem jest masa i to właśnie ją, zgodnie z układem SI, mierzymy w kilogramach. Jak ją zdefiniować? Wbrew pozorom to wcale nie jest takie proste, gdyż zależnie od kontekstu i poruszanego zagadnienia, pojęcie masy potrafi skrywać pewne subtelności. Inaczej je widzi przedstawiciel fizyki klasycznej, inaczej fizyk kwantowy, jeszcze inaczej fizyk relatywistyczny, a jeszcze inaczej nie-fizyk. Jednak na nasze potrzeby w zupełności wystarczająca wydaje się najstarsza i najprostsza z definicji. Mianowicie masa to miara ilości materii. Możemy też bardziej zaszaleć i powtórzyć za Sir Izaakiem Newtonem, że masa to iloczyn gęstości ciała i jego objętości (jednak nie polecam tego wyjaśnienia. Jak zauważył Ernst Mach, gęstość obiektu wyznaczamy znając jego masę, więc taką definicję można sobie w buty wsadzić). Innymi słowy: dużo materii oznacza dużo masy, a mało materii to mało masy.
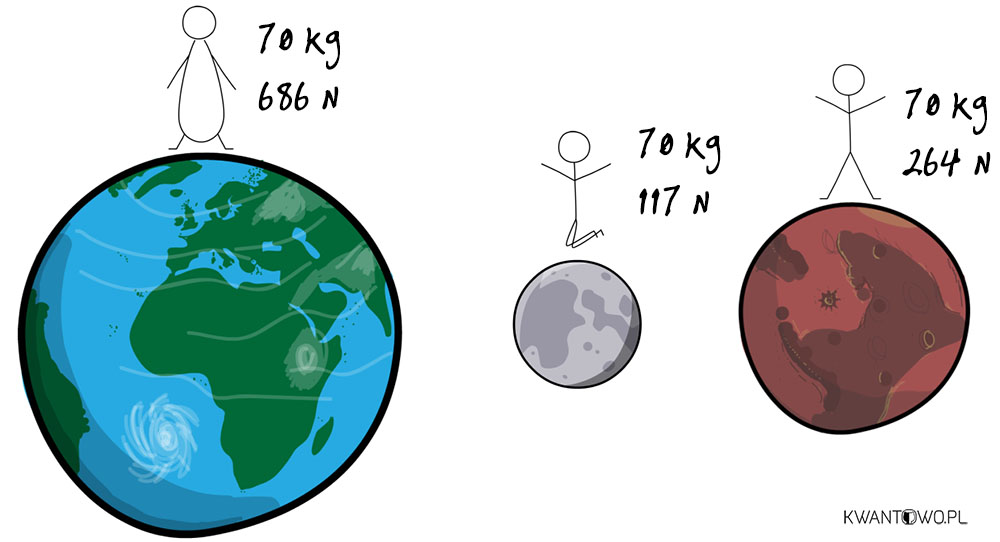
Najistotniejsze jest to, że masa pozostaje właściwością bezwzględną. Ilość materii w Twoim ciele, podobnie jak jego długość, będzie taka sama tu, gdzie siedzisz, na pokładzie Międzynarodowej Stacji Kosmicznej, jak i na Księżycu. Inaczej rzecz ma się z ciężarem, który zależy od masy, ale również od działającej na nas siły przyciągania grawitacyjnego. W związku z tym Twój ciężar na powierzchni Księżyca – przy jego mizernym przyciąganiu – będzie odpowiednio mniejszy niż na Ziemi.
Proste. W zasadzie nie byłoby tu miejsca na żadne pomyłki, gdyby nie fakt, że w języku potocznym lubimy używać obu pojęć zamiennie. Będąc akuratnym, kiedy narzekamy na to, ile przybyło nam kilogramów – powinniśmy mieć na myśli masę. Natomiast zwykła waga łazienkowa określając nasz ciężar, mogłaby podawać wyniki w… niutonach, czyli jednostkach siły. Wtedy wiedziałbyś, że mając masę 70 kg, Twój ciężar wynosi (uwzględniając grawitację Ziemi) jakieś 686 N. Od biedy mógłbyś mówić o 70 kG, czyli kilogramach-siły (jeszcze jedna jednostka, powstała dla odróżnienia od standardowego kilograma).
Kilogram wody
Dajmy sobie jednak już spokój z ciężarem i pozostańmy przy czystej masie. Jak już stwierdziliśmy, mierzymy ją w kilogramach. Lecz skąd kilogram się wziął i jak go wyznaczono? Spróbuj przez moment myśleć jak człowiek wyjęty sprzed kilku stuleci. Nie w głowie nam wyprawy kosmiczne, a nasza wiedza fizyczna ogranicza się do spuścizny Newtona, Galileusza oraz ich poprzedników. Jak uzyskać wiedzę o ilości materii w danym obiekcie?
W zasadzie odpadają wszelkiego rodzaju wagi sprężynowe – wskażą one ciężar. Oczywiście zawieszenie jakiegoś ciała na sprężynie da nam pewną informację, ale wyznaczenie samej masy byłoby dość karkołomne i niewygodne. Znacznie lepszym rozwiązaniem okazuje się najprostsza waga szalkowa. Jej funkcjonowanie polega na porównywaniu poszczególnych ciał. Po jednej stronie kładziemy bryłkę złota, po drugiej np. kurze jajko i załatwione. Zauważ, że możemy tu mówić o pomiarze masy, bowiem gdybyśmy dokonali identycznego doświadczenia na powierzchni Księżyca, odczyt byłby taki sam. Jeśli na Ziemi grudka złota przeważyła jajo, to w każdych warunkach grawitacyjnych zdarzy się to samo. Jeśli obie strony znajdą się w równowadze, to dostrzeżemy to tak na naszej planecie, jak i na Marsie czy na Enceladusie. Metodą zwykłego porównania jesteśmy w stanie wyznaczyć bezwzględną wartość, jaką jest masa.
Teraz wystarczy określić jakiś bardzo konkretny, uniwersalny wzór, do którego zawsze będziemy się odnosić. Tak nasi pradziadowie wpadli na pomysł zdefiniowania kilograma jako równoważności kostki czystej wody o krawędzi 10 centymetrów. Innymi słowy, 1 kg = 1 litrowi czystej wody przy normalnym ciśnieniu i temperaturze. Jeżeli badany obiekt przeważy na wadze 1 litr wody, to bez wątpienia jego masa przekracza 1 kilogram. Błyskotliwe, jak na XVIII wiek.
Wzorzec Kilograma
Starodawna definicja kilograma była całkiem niezła i co ważne, łatwa do ogarnięcia niezależnie od kraju i szerokości geograficznej. Jednak kiedy weźmiemy w rachubę praktykę codzienną, zaczynają się lekkie schody. Trudno żeby na targowiskach całej Europy ganiano z wiadrami i przelewano hektolitry wody, następnie czyniono żmudne obliczenia uwzględniające aktualną temperaturę, ciśnienie oraz masę opakowania. Stąd szybko zaczęto wytapiać poręczne, metalowe odważniki.

Idąc tą drogą, działające w podparyskim Sèvres Międzynarodowe Biuro Miar i Wag, postanowiło stworzyć najdokładniejszy w świecie odważnik mający stanowić wzorzec 1 kilograma. Nie była to idea odosobniona. W owym czasie przygotowano również pręt z platyny i irydu, pełniący rolę wzoru 1 metra. Manifestacja kilograma przybrała kształt 39-milimetrowego cylindrycznego bloczku złożonego z platyny i domieszki irydu. Obiekt przyjął formalną nazwę Międzynarodowego Prototypu Kilograma (IPK), czy też nieoficjalnie Le Grand K i z powodzeniem pełnił swoją rolę nieomal przez 140 lat. Czy komuś to przeszkadzało? Czy jest sens kombinować?
Niestety materia ma tę nieprzyjemną cechę, że jakoś nie bardzo chce być wieczna. Choćbyśmy się dwoili i troili, używali hermetycznych pojemników, dbali o każdy szczegół – czas i tak zawsze zwycięży. Przy każdej dokonywanej co kilka dekad kontroli, zauważano, iż metalowy walec regularnie traci ociupinkę masy. W końcu doszło do tego, że Międzynarodowemu Prototypowi Kilograma brakowało ponad 50 mikrogramów. Jedna z najbardziej podstawowych jednostek miar na świecie, na dobrą sprawę utraciła swoją tożsamość.

W fizyce liczy się stałość
Masa pozostaje zdecydowanie zbyt istotną wielkością, aby świat nauki pozwolił sobie na tak zatrważający brak precyzji. W 2007 roku dwaj amerykańscy profesorowie – Theodore Hill i Ronald Fox – rozpoczęli publiczną agitację za projektem godnego wprowadzenia kilograma w XXI wiek. Pojawiały się różne pomysły, ale jedno nie podlegało dyskusji: Układ SI powinien szukać oparcia wyłącznie w stałych fizycznych. Jeśli nie domyślasz się dlaczego akurat w nich, to zważ na dwie kwestie. Po pierwsze, jak wskazuje nazwa, stała fizyczna to wartość niezmienna w czasie i przestrzeni, która bez jakiegoś kosmologicznego przełomu nie ma prawa ulec zachwianiu. Po drugie, w przeciwieństwie do naszych przodków, mamy aktualnie wszelkie środki konieczne do ultradokładnych pomiarów tychże wartości. Grzechem byłoby więc z tych darów technologii nie skorzystać. Kwestia dotyczy tylko tego, do których stałych się odwołać? W przypadku metra zdecydowano się na prędkość światła w próżni. Zastosowano tu zabawny zabieg, bowiem niejako odwrócono dotychczasowe wyjaśnienie obu pojęć. Najpierw zmierzono, że światło mknie przez przestrzeń z prędkością 299 792 458 metrów na sekundę, a w 1983 roku ustalono, że metr to dystans przemierzany przez światło w czasie 1/299 792 458 sekundy. To bardzo dobre wyjście, bo jak stwierdziliśmy, na prędkości światła można polegać zawsze i w każdych warunkach. W odróżnieniu od kurczącego się z czasem metalowego pręta zalegającego w piwnicach Sèvres.
Pozostało tylko wybrać stałą fizyczną reprezentatywną dla fenomenu masy. W grę od początku wchodziły dwie liczby: stała Avogadra oraz stała Plancka. Amadeo Avogadro znasz zapewne z lekcji chemii i możesz kojarzyć jego nazwisko z pojęciem mola (jednostki, nie owada). Włoch postawił tezę, iż w danej temperaturze i pod stałym ciśnieniem gaz zawiera tę samą liczbę cząsteczek lub atomów, niezależnie od składu chemicznego. Stąd mamy stałą i związaną zeń liczbę Avogadra wynoszącą 6,022 x 1023 cząsteczek na mol. Całkiem atrakcyjny kandydat na fundament definicji masy, ale nie najlepszy.

Pół kilo Plancka

Stała Plancka to nieco bardziej abstrakcyjna wartość, nieobecna w fizyce klasycznej i niewidoczna w naszych codziennych doświadczeniach. Wyłoniła się niemal samorzutnie, podczas formułowania zrębów mechaniki kwantowej przez Maxa Plancka na początku ubiegłego stulecia. Niemiecki uczony postawił hipotezę, jakoby światło było emitowane w pewnych policzalnych porcjach – kwantach. Zgodnie z jego równaniami, energia jednego kwantu powinna być równa iloczynowi częstotliwości światła i pewnej liczby, oznaczonej literą h. To nieprawdopodobnie mała liczba, wynosząca 6,63 x 10-34, gdzie energia jest mnożona przez czas. Planck tak naprawdę nie był przekonany, czy kwanty rzeczywiście istnieją czy może wpadł tylko na matematyczne uproszczenie problemu, ale jego stała była strzałem w dziesiątkę. Bardzo szybko okazała się nieodzownym elementem niemal wszystkich równań rodzącej się fizyki kwantowej.
No dobra, ale jak ma się h do kg? Kluczem do połączenia układanki jest wykonany w 1975 eksperyment Briana Kibble’a i użyta w nim waga watt balance. Jak pewnie się domyślasz, urządzenie Kibble’a w żaden sposób nie przypomina Twojej wagi łazienkowej. W rzeczy samej, watt balance dokonuje pomiaru metalowego odważnika sprzężonego z cewką, przez którą przepuszcza się prąd stały. Przyciąganie grawitacyjne jest równoważone siłą elektromagnetyzmu. Następnie, w drugiej fazie, to cewkę przesuwa się względem ciężarka, co powoduje indukcję napięcia. Jeśli tylko znamy dokładne przyśpieszenie grawitacyjne, właściwości pola elektromagnetycznego oraz rozwiążemy kilka równań – otrzymamy jedyną w swoim rodzaju wagę prądową (więcej na ten temat dowiesz się z kanału Practical Engineering). W odróżnieniu od wagi szalkowej, nie porównujemy masy dwóch fizycznych obiektów, lecz zestawiamy obiekt z pewną, bardzo skrupulatnie dobraną mocą. Gdzie tu miejsce na Plancka? Otóż, aby uzyskać rzeczoną moc używamy prądu elektrycznego, zaś dla osiągnięcia bardzo konkretnej wartości tego prądu, fizycy sięgają do tunelowania Josephsona oraz efektu Halla. Myślę, że nie będziemy w tym miejscu rozpoczynać całego rozdziału dotyczącego tych niełatwych zagadnień, jednak powinieneś mieć świadomość, że oba zjawiska związane są z elektrycznością i oba mają charakter kwantowy. Skoro tak, to rzecz jasna, w opisujących je równaniach figuruje stała Plancka. Dokładna znajomość h, ma zatem bezpośrednie przełożenie na pomiar i definicję masy.

Właśnie w ten sposób, po dość długich latach dyskusji i sporów, otrzymaliśmy ulepszoną definicję jednej z najbardziej przyziemnych jednostek miary. Po naukowemu: 1 kilogram to masa spoczywającego ciała, które w eksperymencie zestawiającym moc mechaniczną i moc elektryczną, daje wartość równą 6,63 x 10-34. Czy wpłynie to na cenę kilograma ziemniaków? Raczej nie. Czy zmieni to cokolwiek? Owszem. Wiele jednostek pozostaje ze sobą w związku, więc poprawienie jednej może wymusić również lifting drugiej. Zmiana definicji kilograma wpłynie chociażby na wielkość niutona, a ten np. na wielkość ampera. Mimo tych niedogodności, reforma kilograma wisiała w powietrzu od dawna i była nieunikniona.










