Każde dziecko wie, że obiekt rzucony do góry musi spaść na ziemię. Cytując klasyka: “Praw fizyki nie zmienisz i nie bądź pan głąb”. Podrzucane jabłko nie uświadamia nam jednak niszczycielskiego potencjału, drzemiącego w tym pozornie niewinnym efekcie.
Bez względu na to czy skorzystamy z klasycznych zasad fizyki newtonowskiej, czy z poprawionej wersji grawitacji autorstwa Einsteina, dojdziemy do analogicznego wniosku: spadający obiekt, w miarę zbliżania do drugiego ciała nabiera prędkości, a tzw. energia potencjalna ulega stopniowemu przekształceniu w energię kinetyczną.

Na pierwszy rzut oka nic ciekawego; spadające z wysokości kilku metrów jabłko czy piłka, budzą emocje porównywalne z meczem polskiej ligi hokeja na trawie. Nieprzypadkowo wielokrotnie pisałem, iż wszechwładna grawitacja to tak naprawdę bardzo słaba siła. Nawet mięśnie dziecka stawiającego swoje pierwsze kroki są w stanie przeciwstawić się przyciąganiu całej naszej planety. Zapomnijmy jednak na chwilę o tym fakcie i wyobraźmy sobie bardziej egzotyczną scenerię, niż orlik lub szkolne laboratorium. Zwykłe, lekkie i niepozorne jabłuszko, nawet w ziemskich warunkach, może okazać się śmiercionośnym pociskiem. Gdybyśmy upuścili owoc z dachu dubajskiego wieżowca Burdż Chalifa, rozbryzgałoby się uderzając w ulicę z prędkością prawie 125 m/s, to jest 450 km/h! (Tak, wiem, że poprawnie powinienem pisać o dżulach a nie prędkości, ale ta druga wartość znacznie bardziej przemawia do wyobraźni.) Oczywiście, pomijając podstawowy hamulec, czyli opór powietrza – tak czy inaczej, nie życzę nikomu przyjmowania takiej dawki energii kinetycznej na główkę.
Ten sam obiekt, spadając z podobnej wysokości ~800 metrów na powierzchnię Słońca – zakładając ultraodporność naszego jabłka na ekstremalne temperatury i ciśnienia – rozpędziłby się do ponad 650 m/s (2340 km/h). To jednak nadal wielkości wręcz śmiesznie małe w kosmicznej skali. Jeśli weźmiemy pod lupę ciało mknące ku naszej gwieździe z wysokości tysiąca kilometrów, to wreszcie otrzymamy imponujący z ludzkiej perspektywy wynik 23 km/s, czyli 84 tysięcy km/h. Trudno sobie wyobrazić cokolwiek frunącego z takim impetem w ziemskich warunkach, ale pamiętajmy, że to nadal mniej niż choćby prędkość ruchu obiegowego naszej planety, wynoszącej niecałe 30 km/s.
Teraz, aby było ciekawiej, przenieśmy się o 8 lat świetlnych, w okolice gwiezdnego układu podwójnego Syriusza. W analogicznym doświadczeniu do poprzedniego, dla majestatycznego Syriusza A prędkość spadającego jabłka wyniesie 138 km/s – prawie pół miliona kilometrów na godzinę. Nieźle, ale paradoksalnie to i tak nic wielkiego wobec wygrzewającego stare kości, niewielkiego Syriusza B. Ledwie dostrzegalny w blasku swego towarzysza biały karzeł jest setki razy mniejszy, ale zaledwie dwukrotnie mniej masywny. Stosując charakterystyczny dla Alberta Einsteina schemat myślowy, możemy wyobrazić sobie dewastację czasoprzestrzennej sieci, jaką wywołuje to maleństwo. Wcześniej mogliśmy mówić o czymś w stylu grawitacyjnej zjeżdżalni, ale w przypadku tak upakowanej masy to już raczej lej o stromych ścianach. Dlatego upuszczone w okolicach tysiąca kilometrów od Syriusza B jabłko w mgnieniu oka zostanie rozsmarowane na jego powierzchni, przy prędkości liczonej w tysiącach kilometrów na sekundę! Jeśli przyjmiemy wielkość 7 tysięcy km/s to nasze niepozorne jabłuszko walnie z energią ponad 12 milionów gigadżuli, czy bardziej obrazowo niecałych trzech megaton – z mocą małego ładunku termojądrowego.
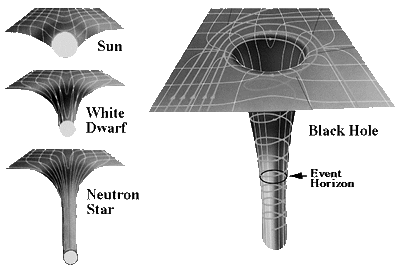
Pewnie przeczuwacie, że pozostały jeszcze tylko dwa bardziej skrajne typy obiektów. Pierwszy to gwiazda neutronowa, której doskonały przykład stanowi oddalony o dziesięć tysięcy lat świetlnych PSR 1257+12. Badany przez Aleksandra Wolszczana pulsar jest tylko trochę masywniejszy od Syriusza B, ale jeszcze o wiele bardziej gęsty. O ile biały karzeł dysponuje masą przeciętnej gwiazdy przy gabarytach podobnych Ziemi, o tyle zdegenerowana materia gwiazdy neutronowej mieści się w kuli o średnicy kilkunastu kilometrów. Ściany grawitacyjnej studni są jeszcze bardziej spadziste; a hipotetyczne jabłko mogłoby rozpędzić się niemalże do 100 tysięcy km/s. Taka energia byłaby w stanie siać zniszczenie porównywalne z meteorytem tunguskim. Co równie istotne, wreszcie dochodzimy do spieniających czasoprzestrzeń prędkości relatywistycznych, bliskich 1/3 prędkości światła.
A co z czarnymi dziurami? Tu sprawa robi się znacznie poważniejsza. Jak powszechnie wiadomo zewnętrzna warstwa czarnej dziury, zwana horyzontem zdarzeń, to granica spoza której nie mogą uciec nawet fotony. Dla naszego eksperymentu myślowego oznacza to tyle, że lgnący w ramiona kosmicznego potwora przedmiot, przyśpieszy do maksymalnej możliwej prędkości. Horyzont nie stanowi jednak materialnej ściany, toteż jabłko będzie spadać dalej, kierując się w stronę zagadkowej osobliwości, umiejscowionej w samym centrum dziury.
Czy dojdzie zatem do dalszego przyśpieszania? Raczej nie. Prawdopodobnie będziemy mieli do czynienia z procesem podobnym do tego, zachodzącego podczas akceleracji cząstek elementarnych. Kiedy naukowcy z LHC rozpędzają protony, mogą nieustannie zwielokrotniać wykorzystywaną energię, ale cząstka będzie jedynie dążyć do osiągnięcia prędkości światła, nigdy do niej nie dochodząc. Czarna dziura to jednak ewenement. Czy stanie się z jabłkiem po minięciu horyzontu zdarzeń? Czy materia przekroczy granicę 300 tysięcy km/s? A może wewnątrz czarnej dziury dochodzi do kompletnego demontażu zasad fizyki, którym hołdujemy na co dzień i nasze rozważania mijają się z celem? To już tylko domysły.