Popularnonaukowe

Geometryczne niebo perfekcjonistów. Sekrety 5 brył (nie)platońskich

Bryły platońskie mają w sobie coś pociągającego. Nie dość, że cechuje je niedefiniowalna elegancja, to jeszcze tworzą ekskluzywny klub, mieszczący po wsze czasy zaledwie pięciu członków.

byAdam Adamczyk

13/02/2022

5 minute read

7 komentarzy

Wstydliwa tajemnica La Géode

Zanim przejdziemy do gadaniny o matematyce i geometrii proponuję, żebyśmy wykonali mały skok w kierunku architektury. Interesować nas będzie pewien szczególny gmach, należący do paryskiego Miasta Nauki i Przemysłu, znany wśród miejscowych jako La Géode. Jest to siedziba kina, przypominająca z dystansu osobliwą, 36-metrową lustrzaną sferę. Dopiero dokładniejszy rzut oka na konstrukcję zdradza, że jej gładka powierzchnia nie jest jednorodna, lecz powstała z połączenia tysięcy płyt o kształcie trójkąta.

Jeżeli obejdziemy Geodę dookoła i cierpliwie przeanalizujemy rozłożenie trójkątów, zauważymy coś jeszcze. Bryła nie jest wcale doskonała i niepostrzeżenie, gdzieś po drodze, gubi swoją regularność. Uważny turysta wydedukuje w końcu, że problem stanowią punkty styku trójkątnych kafelków. Nie są one identyczne. O ile w zdecydowanej większości miejsc spotykają się wierzchołki sześciu płyt, o tyle niektóre punkty łączą w sobie tylko po pięć trójkątów.

La Géode w Paryżu — Gmach *La Géode* należący do paryskiego kompleksu *Cité des Sciences et de l’Industrie*. W rzeczywistości kopuła o średnicy 36 metrów jest zlepkiem kilku tysięcy trójkątnych płyt.

Może to wyglądać na fuszerkę albo objaw lenistwa, ale w rzeczywistości było gruntownie przemyślanym zabiegiem budowniczych. Architekt nie mógł zaprojektować foremnego wielościanu złożonego z 6433 trójkątów równobocznych, stykających się w każdym punkcie w ten sam sposób i pod dokładnie tym samym kątem. Nie mógł, ponieważ jest to geometrycznie po prostu niewykonalne.

Wszystko w związku z pewnym ograniczeniem, z którego matematycy zdają sobie sprawę od ponad dwóch tysięcy lat.

Figury platońskie na płasko i w 3D

Problem, o którym mowa dotyczy tylko i wyłącznie brył. Rozważając dwuwymiarowe wielokąty foremne – płaskie figury o bokach identycznej długości, stykających się pod identycznymi kątami – szybko dojdziemy do wniosku, że podobne obostrzenie nie obowiązuje. Bez trudu możemy naszkicować na kartce papieru trójkąt równoboczny, kwadrat, pięciokąt foremny, sześciokąt, siedmiokąt, ośmiokąt, dziewięciokąt, dwudziestokąt, stukąt… I tak bez końca, aż rysowany kształt upodobni się do eleganckiego okręgu.

Skoro mamy do dyspozycji nieskończoną liczbę wielokątów foremnych, spróbujmy przejść w trójwymiar. Aby otrzymać wielościan foremny, musimy wybrać odpowiednie wielokąty i złożyć je w taki sposób, aby w każdym wierzchołku zbiegała się taka sama liczba krawędzi, pod tożsamym kątem^[1]I niech to będzie taki kąt, aby powstała bryła była wypukła. W innym wypadku otrzymamy dziwadło w rodzaju ośmiościanu gwiaździstego.. Kryteria nie brzmią na zbyt wyszukane, ale jeśli zechcemy własnoręcznie złożyć tego rodzaju pudełko, szybko zrozumiemy, że większość figur nie pozwoli nam na wykonanie zadania. Eliminując kolejne opcje, jedna po drugiej, pozostaniemy ze skromnymi pięcioma bryłami.

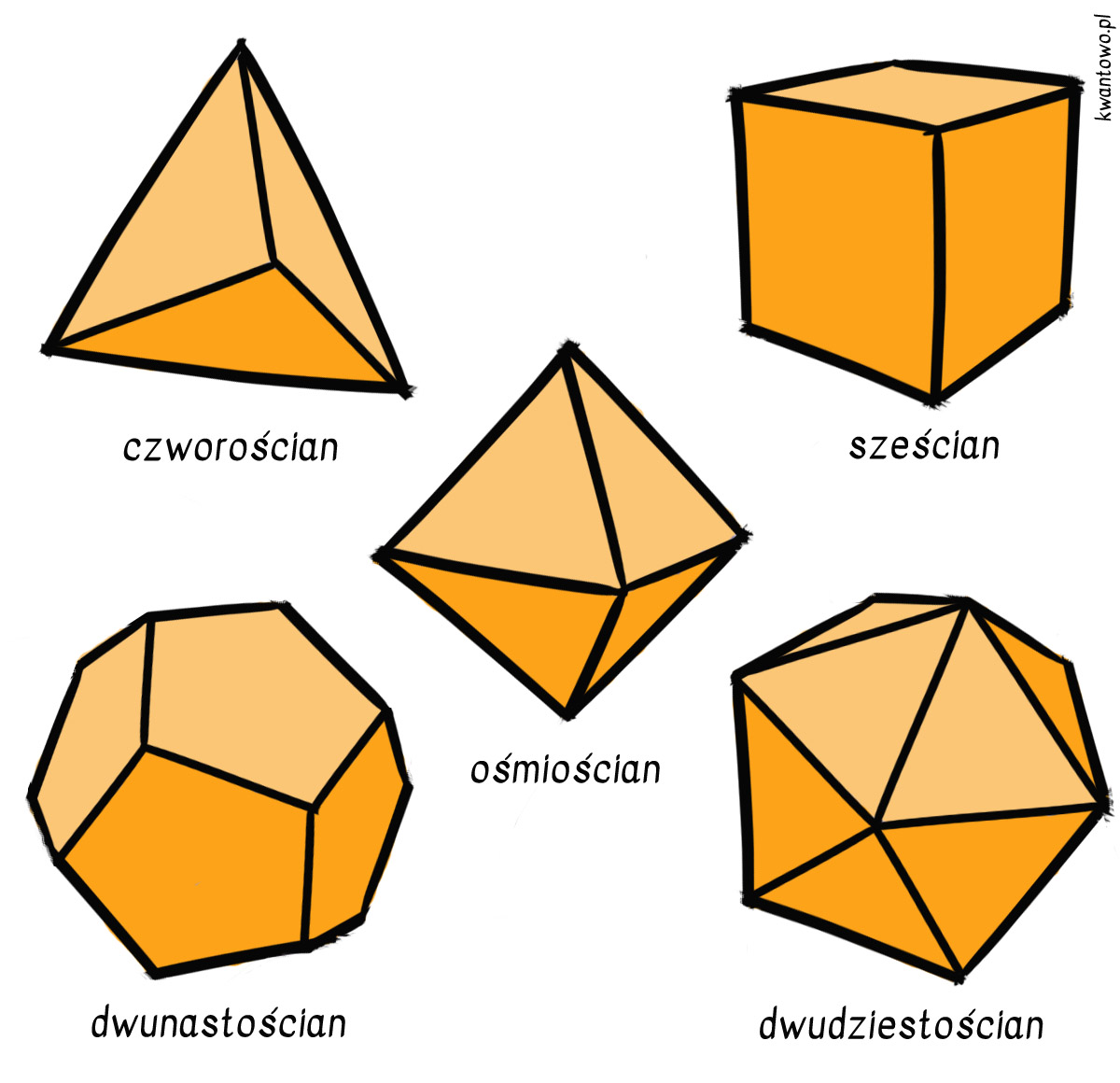
Bryły platońskie to zamknięty zbiór mieszczący zaledwie pięć obiektów: czworościan, ośmiościan i dwudziestościan składające się z odpowiednio połączonych trójkątów równobocznych, sześcian złożony z kwadratów, a także dwunastościan zbudowany z pięciokątów foremnych.

Są to: czworościan, sześcian, ośmiościan, dwunastościan oraz dwudziestościan. Jeśli chcecie brzmieć, jakbyście używali pradawnych inkantacji, możecie również sięgnąć do terminologii greckiej i mówić o tetraedrach, heksaedrach, oktaedrach, dodekaedrach oraz ikosaedrach.

Platon i zapomniany Teajtet

Powyższy fakt jako pierwszy odnotował pewien starożytny uczony i – uwaga – nie nazywał się Platon. To jeden z uczniów sławnego filozofa, niejaki Teajtet z Aten, jako pierwszy sformułował katalog wypukłych wielościanów foremnych i już 2400 lat temu zastrzegł, że jest to lista po wsze czasy zamknięta. Nie mylił się.

Dlaczego zatem w szkole poznajemy bryły platońskie? Być może przez legendę Platona, która każe przypisywać mu również prace jego zdolnych wychowanków. A może dlatego, że myśliciel wykorzystał pomysł Teajteta do skomponowania kompleksowej, oryginalnej wizji wszechświata, co dla ówczesnych stanowiło zapewne bardziej spektakularne osiągnięcie niż postawienie prostego twierdzenia.

Zresztą, należy oddać Platonowi, że jego idea rzeczywiście mogła robić wrażenie wyjątkowo trzeźwej i logicznej – przynajmniej jak na standardy starożytności. Grek zakładał, że cała fizyczna rzeczywistość to mieszanina czterech żywiołów: ognia, wody, ziemi i powietrza. Każdy z żywiołów w najmniejszej skali miał być złożony z atomów, które z kolei przyjmowały kształty – tak, dobrze przeczuwacie – wielościanów foremnych. Wedle tej koncepcji, maleńkie dwudziestościany, najbliższe kuli, tworzyły wodę; sześciany składały się na ziemię; powietrze to lekkie ośmiościany; natomiast płomień to nic innego, aniżeli zbiór ostrych i nieprzyjemnych w dotyku czworościanów.

Wolny pozostawał dwunastościan. Taką formę według Platona musiał przyjmować cały istniejący wszechświat. Nie zgadzał się z nim Arystoteles, podejrzewający, że liczba brył platońskich zwiastuje istnienie jeszcze jednego, nieznanego atomu. Dodatkowy żywioł był nieobecny na Ziemi, ale mógł stanowić materię gwiazd i innych ciał niebieskich.

Ale dlaczego pięć brył?

Od czasów antycznej Grecji świat poszedł odrobinę do przodu. Żywioły od dawna nie są uznawane za esencję wszechświata, a wśród wizji starożytnych mędrców na próżno szukać kwantowomechanicznych podstaw funkcjonowania atomów. Może więc powinniśmy założyć, że również Teajtet coś przeoczył i przedwcześnie ograniczył liczbę wielościanów foremnych do pięciu?

Jaki jest właściwie konkretny powód tego restrykcyjnego obostrzenia?

Żeby to zrozumieć rozważmy dla przykładu wszystkie bryły platońskie zbudowane na bazie trójkąta równobocznego. Najpierw mamy czworościan, gdzie w każdym wierzchołku stykają się ze sobą trzy trójkąty. Następnie ośmiościan, w którym każdy wierzchołek łączy cztery trójkąty. Wreszcie w wierzchołkach dwudziestościanu spotyka się po pięć trójkątów. Idąc tym tropem dalej, powinniśmy podjąć próbę zetknięcia w jednym punkcie sześciu trójkątów. Co się wtedy stanie? Spokojnie, nie jest to w żaden sposób zabronione i możemy podjąć taką próbę, a wszechświat nie eksploduje. Tyle tylko, że w wyniku takiej operacji nie otrzymamy wcale kolejnej bryły, lecz… podział płaszczyzny.

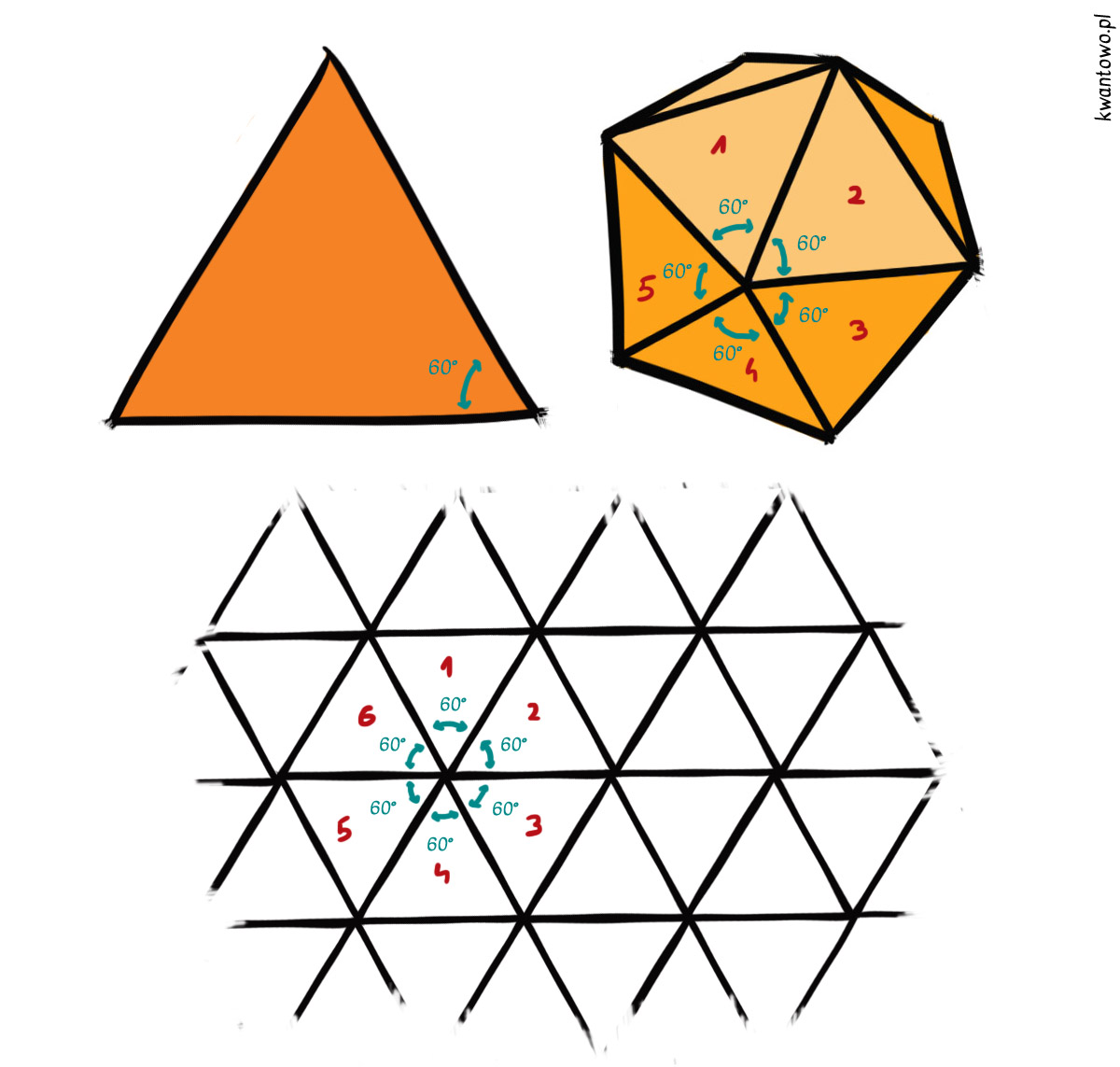
Kąty w przestrzeni i bryle platońskiej — Mając do dyspozycji trzy, cztery lub pięć trójkątów równobocznych, możemy z nich zbudować wielościany foremne, jednak dorzucając jeszcze jeden trójkąt wracamy do dwóch wymiarów i zamiast bryły otrzymujemy *powierzchnię platońską*.

Powód, dla którego powracamy do świata dwóch wymiarów ma związek z kątem, pod jakim łączą się ściany. Każdy dodatkowy trójkąt zwiększa ten kąt o 60 stopni i przy sześciu trójkątach przypadających na wierzchołek, staje się on równy 360 stopniom. Krzywizna znika, dostajemy płaszczyznę. Nie inaczej będzie, jeśli podejmiemy próbę połączenia czterech kwadratów lub czterech sześciokątów. Dlatego nie ma mowy o wyjątkach. Klub brył platońskich pozostaje ekskluzywny i nie przyjmuje nowych członków.

A co jeżeli postanowimy za wszelką cenę zanurzyć się w odmęty geometrycznej dewiacji i mimo wszystko dołożymy siódmy trójkąt i kolejne? Będzie to oznaczało przekroczenie bariery 360 stopni, co sprawi, że dotychczasową gładką płaszczyznę zastąpi niechlujna, pomiętolona struktura. Oczywiście wśród matematyków nie brakuje miłośników takich oryginalnych kształtów. Niektórzy, jak Henry Segerman z Oklahomy, obsypują nimi internet, a nawet próbują je odtwarzać na drukarkach 3D.

Osiem trójkątów złączonych wierzchołkami — To się stanie, jeśli spróbujecie zetknąć wierzchołkami więcej niż sześć trójkątów równobocznych – powykręca wam oczy.

Dwudziestościan w kulę zaklęty

Zakaz sformułowany przez Teajteta stoi również za zagadkową nieregularnością La Géode. Adrien Fainsilber – projektant francuskiej budowli – za żadne skarby nie był w stanie stworzyć foremnego 6433-ścianu, więc uciekł się do genialnej geometrycznej sztuczki. Wyszedł od kształtu (ściętego) platońskiego dwudziestościanu, po czym go “nadmuchał”, nadając całości miłą dla oka, kulistą formę.