Nobel z fizyki 2021 – Porządkowanie nieporządku

Tegorocznym Noblem w dziedzinie fizyki podzielili się Syukuro Manabe, Klaus Hasselmann oraz Giorgio Parisi. Nie tworzą żadnego zespołu i prawdopodobnie nigdy nie mieli szansy ze sobą współpracować. Japończyk to fizyk atmosfery, pionier, który już sześćdziesiąt lat temu zaczął wykorzystywać wielkie jak szafa komputery do tworzenia modeli klimatycznych. Hasselmann również specjalizuje się w badaniach klimatu, choć jego dorobek dotyczy raczej oceanów oraz wzajemnych zależności na linii ocean-atmosfera. Jedna z publikacji Niemca legła u podstaw tezy o antropogenicznym charakterze obserwowanego wzrostu temperatury.

Coś więcej niż klimat

Jednak spłycenie sprawy do chwytliwego nagłówka Nobel za klimat nie oddaje głębi oraz uniwersalności docenionych prac. Takie uproszczenie pozostawia również na uboczu ostatniego spośród laureatów, czyli Giorgiego Parisiego.

Włoski teoretyk może wydawać się wyrwany z zupełnie innej bajki, jako autorytet w dziedzinie chromodynamiki kwantowej (QCD), kwantowej teorii pola oraz fizyki materii skondensowanej. A jednak, studiując zachowanie potężnych zbiorów cząstek, atomów i molekuł, w pewnym sensie Parisi zderzył się z tą samą przeszkodą, co jego starsi koledzy^[1]Manabe i Hasselmann to rówieśnicy obchodzący 90. urodziny. Ale i tak zdają się młodzieniaszkami przy Arthurze Ashkinie, który w momencie otrzymania Nobla miał na karku 96 lat., próbujący ogarnąć subtelności kształtujące klimat naszej planety.

Wszyscy ci uczeni musieli zmierzyć się przygniatającą złożonością układów fizycznych. Tyle, że w różnej skali.

Szkło, które nie było szkłem

Wiem, nie brzmi to zbyt podniecająco. Zwłaszcza w zestawieniu z czarnymi dziurami, planetami pozasłonecznymi, bozonem Higgsa, czy falami grawitacyjnymi – honorowanymi w Sztokholmie w przeszłości. Ale może to kwestia niezbyt atrakcyjnego opakowania? A co, gdybym powiedział^[2]Ale mówię cicho, bo sofony słuchają…, że rzecz dotyczy problemu n-ciał? Znanych każdemu ze szkoły ruchów Browna? Albo słynnego efektu motyla? Bo tak się składa, że zainteresowania trzech sędziwych uczonych leżą mniej więcej w tym obszarze. Gdzieś na pograniczu fizyki i matematycznego królestwa chaosu.

O wyróżnieniu dla klimatologów napisano już chyba wszystko, więc proponuję poświęcić kilka akapitów bardziej zaniedbanemu Parisiemu. Choć teoretyk przez lata uchodził przede wszystkim za specjalistę od kwarków i gluonów, dla Akademii istotniejsze były jego późniejsze prace, dotyczące osobliwego rodzaju materii nazywanego szkłem spinowym.

Giorgio Parisi otrzymał Nobel z fizyki 2021 — Giorgio Parisi, profesor rzymskiego Uniwersytetu La Sapienza i współlaureat Nagrody Nobla z fizyki 2021.

Wbrew nazwie, nie chodzi tu wcale o przezroczystą, kruchą substancję, z jakiej wykonane są szyby, szklanki i okulary. Niecni uczeni zwykli takim mianem określać substancje (np. stopy niektórych metali) o bardzo specyficznej charakterystyce, które skojarzyły im się z właściwościami szkła. Uprzedzam, że jest to dość pokrętne skojarzenie.

Gdybyśmy wzięli pod lupę większość metali (i nie tylko) naszym oczom ukazałby się uporządkowany obraz sieci krystalicznej. Jeśli jednak zbadamy w podobny sposób np. ściankę kufla piwa, dojrzymy niedoskonałą plątaninę molekuł, które niczym mieszkańcy Pompejów zastygły w przypadkowych pozycjach, zaskoczone nagłą zmianą warunków. Tym samym, pod względem struktury szkło przypomina bardziej zatrzymaną w czasie ciecz, niż typowe ciało stałe.

W przypadku szkła spinowego nie interesuje nas jednak bałaganiarskie upakowanie cząsteczek, lecz losowe rozłożenie spinów (stąd nazwa), co przekłada się na egzotyczne właściwości magnetyczne materiału.

Co frustruje atomy?

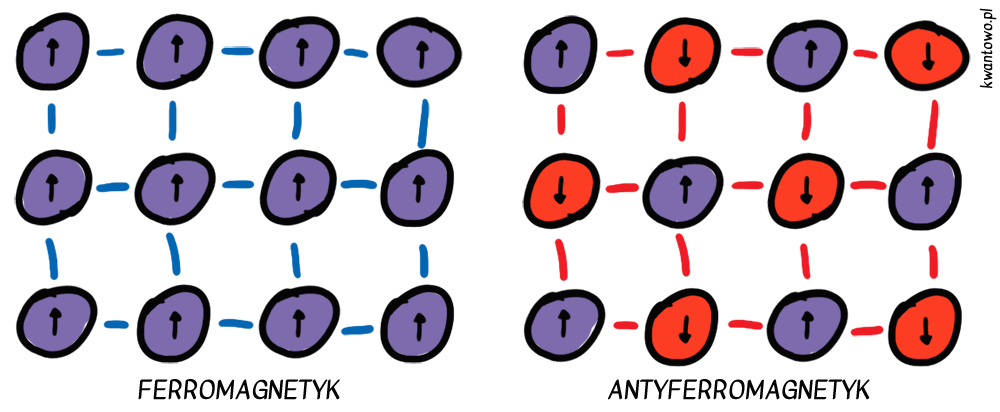
Na czym polega ta egzotyka? W pospolitym żelazie obszary namagnesowania – działające jak osobne mikroskopijne magnesiki – orientują się w tym samym kierunku. Mówimy w takim przypadku o materiale ferromagnetycznym. Jego przeciwieństwem będzie antyferromagnetyk, gdzie sąsiadujące magnesiki pozostają ułożone na przemian. Szkło spinowe jest znacznie zabawniejsze, ponieważ łączy elementy ferro i antyferromagnetyczne. W takim materiale wszystkie atomy (lub cząsteczki) są poobracane względem siebie w różnorodny sposób, co przez długi czas zdawało się fizykom stanem zupełnego chaosu.

Ferromagnetyk i antyferromagnetyk — Wzajemne ustawienie spinów atomów lub cząsteczek w materiale ferromagnetycznym i antyferromagnetycznym.

W rzeczywistości zachowaniem spinów rządzą pewne reguły, które Giorgio Parisi wraz z kolegami wyrazili w postaci zaawansowanych równań różniczkowych. Na nasze szczęście Włoch ma też duszę poety i potrafił również sprowadzić cały problem do szekspirowskiej tragedii. W metaforze tej mamy do czynienia ze skomplikowaną relacją, gdzie główny bohater próbuje zacieśnić przyjaźń z dwoma postaciami, które się wzajemnie nienawidzą. Zdobywając względy pierwszej, ryzykuje sympatię drugiej. Sytuacja niezbyt komfortowa, żeby nie powiedzieć frustrująca. I tak też, w kontekście szkła spinowego, fizycy mówią o frustracji spinów.

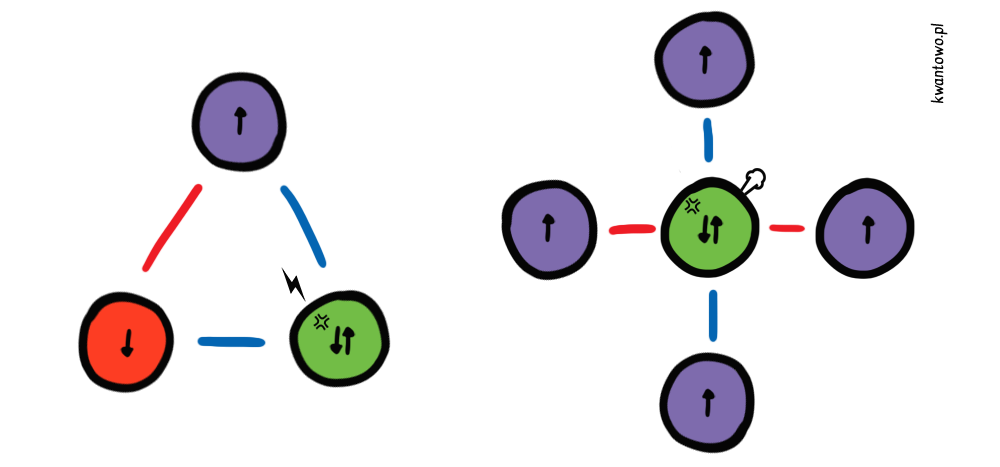
Gra w szkło spinowe

Możemy również wyobrazić sobie ten problem w formie geekowskiej gry planszowej. Podczas zabawy mamy do dyspozycji planszę z miejscami na żetony (atomy), od których odchodzą linie stanowiące miejsca na podłużne klocki o kolorze niebieskim (symbolizujące wiązanie ferromagnetyczne) lub czerwonym (antyferromagnetyczne). Zasada jest taka, że każde czerwone połączenie zabiera punkt energii, a każde niebieskie punkt dodaje. Jeżeli sumaryczna energia przypadająca na żeton będzie ujemna to konfiguracja zachowa stabilność, jeżeli dodatnia to gracz musi wykonać ruch, co oczywiście poskutkuje rozlaniem zmian po całej sieci.

Gra planszowa o szkle spinowym — Pewnie myśleliście, że to tylko niezbyt przemyślana metafora? Tymczasem gra planszowa pod tytułem *Spin Glasses: The Game* kilka lat temu naprawdę trafiła do niemieckich sklepów.

To rzecz jasna bardzo prymitywne wyobrażenie spinowego bałaganu. W rzeczywistości nie mamy przecież do czynienia z przejrzystą płaszczyzną, zaledwie dwoma ułożeniami spinów i kilkunastoma żetonami, lecz z trójwymiarowym układem kwantowym, gdzie każdy z milionów atomów nieustannie szuka dla siebie najbardziej komfortowej pozycji. To właśnie wykucie matematycznych narzędzi umożliwiających wypatrzenie konkretnych reguł w złożonym systemie spinów tak zaimponowało Komisji Noblowskiej. I słusznie, bo jak zauważono w uzasadnieniu, odpryski metody Parisiego mogą odnaleźć zastosowanie również daleko poza fizyką, w biologii, neuronauce oraz uczeniu maszynowym.

Zapanować nad spinowym chaosem

W tym miejscu docieramy do punktu, gdzie rozważania nad szkłem spinowym spotykają się z próbami modelowania klimatu planety. Na pierwszy rzut oka oba tematy łączy niewiele, ale sięgając sedna zauważymy, że operujemy po prostu na arcyzłożonych systemach fizycznych, obejmujących trudną do ogarnięcia liczbę składników. A gdzie duża liczba składników i danych, tam niesłychana wrażliwość systemu na każde, nawet najdrobniejsze zaburzenie. Zmiana jednego parametru, przesunięcie pojedynczego elementu, ruch skrzydłem metaforycznego motyla – może wystarczyć do zdewastowania skrzętnie formułowanej prognozy. Czyni to analizowany układ chaotycznym^[3]Mogę tylko zgadywać, że gdyby żył nadal Edward Lorenz, prawdziwy pionier teorii chaosu i odkrywca efektu motyla, również doczekałby się Nobla..

Ktoś mógłby w tym momencie zaprotestować. Przecież komplet danych o wybranych obiektach i znajomość ścisłych prawideł fizyki, powinny wystarczyć do dokładnego przewidzenia ewolucji systemu. W teorii tak, ale… jak to wszystko ogarnąć? Nikt nie jest w stanie zmierzyć z nieskończoną precyzją stanu każdej skały w Układzie Słonecznym, każdego grama wody w oceanie, każdej molekuły powietrza, ani każdego atomu szkła spinowego. A nawet gdybyśmy posiedli wszechwiedzę godną demona Maxwella, to nie istnieje komputer pozwalający na zgromadzenie i przemielenie tych wszystkich danych.

Właśnie dlatego, że mówimy o czymś technicznie niewykonalnym, tak cenne stają się wszelkie sztuczki pozwalające na obejście naszych ograniczeń^[4]Dość dosłownie, bo od strony matematycznej, Parisi użył na swoje potrzeby metody nazywanej sztuczką z repliką (ang. replica trick).. Badając złożony układ nie próbujemy więc monitorować każdej jego cząstki. Zamiast tego szukamy uproszczeń. Bierzemy w rachubę tylko wycinek złożonej struktury, identyfikujemy najważniejsze reguły gry, sięgamy do statystyki i próbujemy symulować rzeczywistość.

Tak powstają modele na tyle realistyczne, aby dawały zadowalające wyniki, ale dość ogólne, żebyśmy mogli wykorzystać je w praktyce.